Redes Neuronales aplicadas a Series Temporales¶
Objetivo¶
El objetivo de este cuaderno es introducir algunos ejemplos de ajuste de redes neuronales en el contexto de análsiis de series temporales. En particular:
Discutir cómo convertir el problema de ajuste de modelos a un problema de aprendizaje supervisado.
Analizar la relación entre RNN clásicas y los modelos lineales ya vistos.
Discutir algunos ejemplos más complejos de redes (CNN, RNN, LSTM).
Observar cómo se puede realizar la predicción.
Nos basaremos en la biblioteca tensorflow, por lo que es necesario una instalación de Python con tensorflow para que funcione. En particular usaremos la biblioteca keras para interactuar de manera sencilla con tensorflow
Ejemplo¶
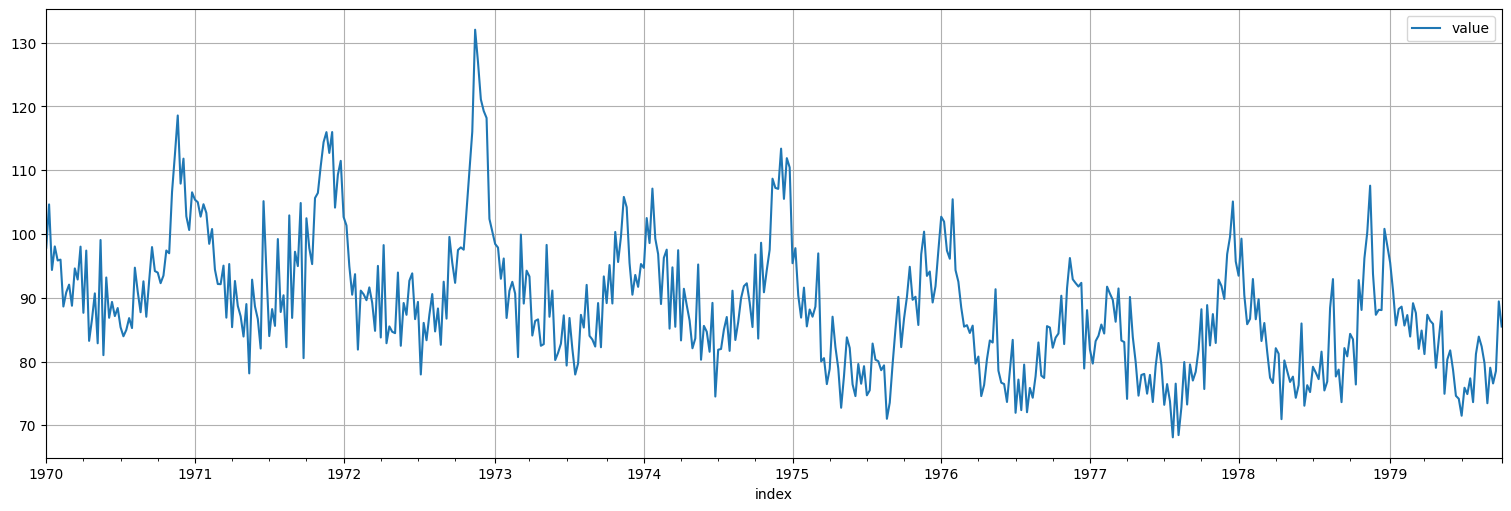
Trabajaremos en un principio con la serie de mortalidad que ya vimos:
cmort = astsa.cmort
cmort.plot();
Estacionarización¶
Como vimos antes, resulta útil llevar primero la serie a algo estacionario. En este caso, le quitamos la tendencia.
from statsmodels.formula.api import ols
time = pd.Series([idx.ordinal for idx in cmort.index], index=cmort.index, name="Semana")
data = pd.concat([cmort, time], axis=1).dropna()
fit = ols(formula="cmort~time", data=data).fit()
fit.summary()
| Dep. Variable: | cmort | R-squared: | 0.211 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.209 |
| Method: | Least Squares | F-statistic: | 135.0 |
| Date: | Wed, 12 Jun 2024 | Prob (F-statistic): | 8.03e-28 |
| Time: | 19:43:45 | Log-Likelihood: | -1829.9 |
| No. Observations: | 508 | AIC: | 3664. |
| Df Residuals: | 506 | BIC: | 3672. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 96.6510 | 0.790 | 122.335 | 0.000 | 95.099 | 98.203 |
| time | -0.0312 | 0.003 | -11.618 | 0.000 | -0.036 | -0.026 |
| Omnibus: | 67.579 | Durbin-Watson: | 0.576 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 97.699 |
| Skew: | 0.906 | Prob(JB): | 6.09e-22 |
| Kurtosis: | 4.156 | Cond. No. | 590. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
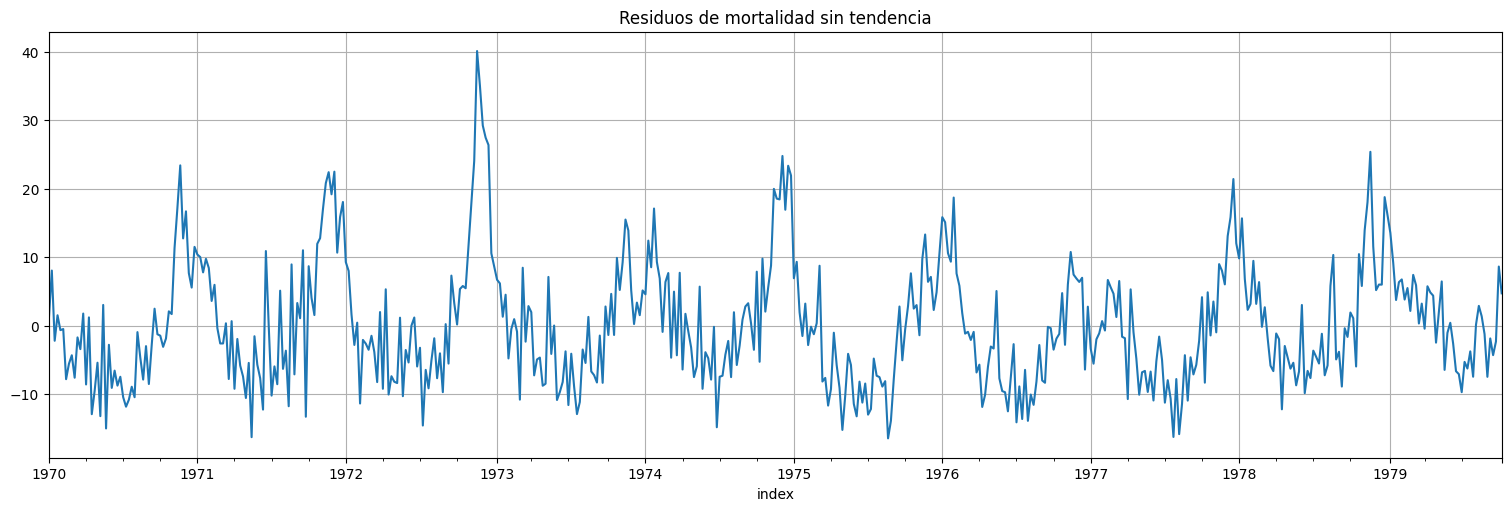
x=fit.resid
x.plot()
plt.title("Residuos de mortalidad sin tendencia");
Aprendizaje en series temporales¶
Las redes neuronales sirven para realizar aprendizaje supervisado, esto es, a partir de ejemplos, encontrar los coeficientes de la red que minimizan una función de loss o pérdida. En este caso:
Los ejemplos son “ventanas” de valores en el tiempo de la serie, y uno o más features que nos interese incorporar:
Por ejemplo, el valor de la semana del año en este caso importa debido a la variación anual.
Pueden ser también diferentes “features” como la temperatura y partículas que ya vimos.
El valor a predecir es por ejemplo, el siguiente valor de la serie, o una ventana hacia adelante.
En base a esto, se arma una arquitectura de red y se entrena usando backpropagation.
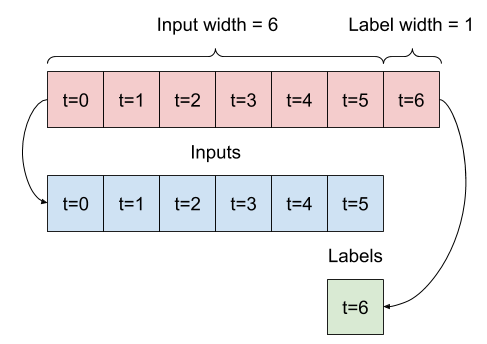
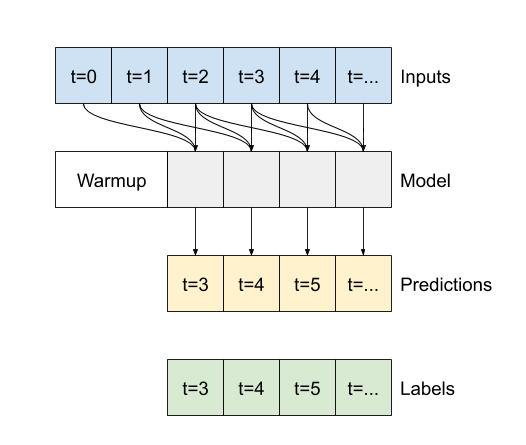
Diagrama¶
Para el caso por ejemplo de tomar 6 lags:
Preprocesamiento¶
En este caso, haremos varios modelos. El primero simplemente usa como feature la propia serie, usando una cantidad window de lags hacia atrás. Separamos ademas una parte para testear predicciones.
Ahora debemos rearmar los datos para el formato tensorflow:
Cada feature es un vector conteniendo una ventana de
windowdatos de la serie.Cada valor observado es un vector (en este caso escalar) con los datos a predecir
pred.
La función keras.utils.timeseries_dataset_from_array() nos permite hacer esto ordenado (aunque con algunos pitfalls):
window = 3 #lags a mirar
input_data = x.values[:-window]
targets = x.values[window:]
dataset = keras.utils.timeseries_dataset_from_array( input_data, targets,
sequence_length=window,
batch_size=16)
train, test = keras.utils.split_dataset(dataset,0.8)
2024-06-12 19:57:22.267907: W tensorflow/core/framework/local_rendezvous.cc:404] Local rendezvous is aborting with status: OUT_OF_RANGE: End of sequence
train.as_numpy_iterator().next()
(array([[ 1.23010434, 8.05125614, -2.19759207],
[ 8.05125614, -2.19759207, 1.52355972],
[ -2.19759207, 1.52355972, -0.64528849],
[ 1.52355972, -0.64528849, -0.4841367 ],
[ -0.64528849, -0.4841367 , -7.8029849 ],
[ -0.4841367 , -7.8029849 , -5.55183311],
[ -7.8029849 , -5.55183311, -4.31068132],
[ -5.55183311, -4.31068132, -7.58952953],
[ -4.31068132, -7.58952953, -1.70837773],
[ -7.58952953, -1.70837773, -3.41722594],
[ -1.70837773, -3.41722594, 1.77392585],
[ -3.41722594, 1.77392585, -8.57492236],
[ 1.77392585, -8.57492236, 1.21622943],
[ -8.57492236, 1.21622943, -12.91261877],
[ 1.21622943, -12.91261877, -9.52146698],
[-12.91261877, -9.52146698, -5.40031519]]),
array([ 1.52355972, -0.64528849, -0.4841367 , -7.8029849 ,
-5.55183311, -4.31068132, -7.58952953, -1.70837773,
-3.41722594, 1.77392585, -8.57492236, 1.21622943,
-12.91261877, -9.52146698, -5.40031519, -13.1991634 ]))
Modelo 1: una única neurona densa.¶
Esto, sin agregar no linealidades, debería coincidir con el modelo autorregresivo que ya vimos.
model = keras.Sequential([
keras.Input(shape=(window,)),
keras.layers.Dense(units=1)
])
model.summary()
Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_1 (Dense) │ (None, 1) │ 4 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 4 (16.00 B)
Trainable params: 4 (16.00 B)
Non-trainable params: 0 (0.00 B)
model.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model.fit(
train,
epochs=300,
verbose=False,
validation_data=test
)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
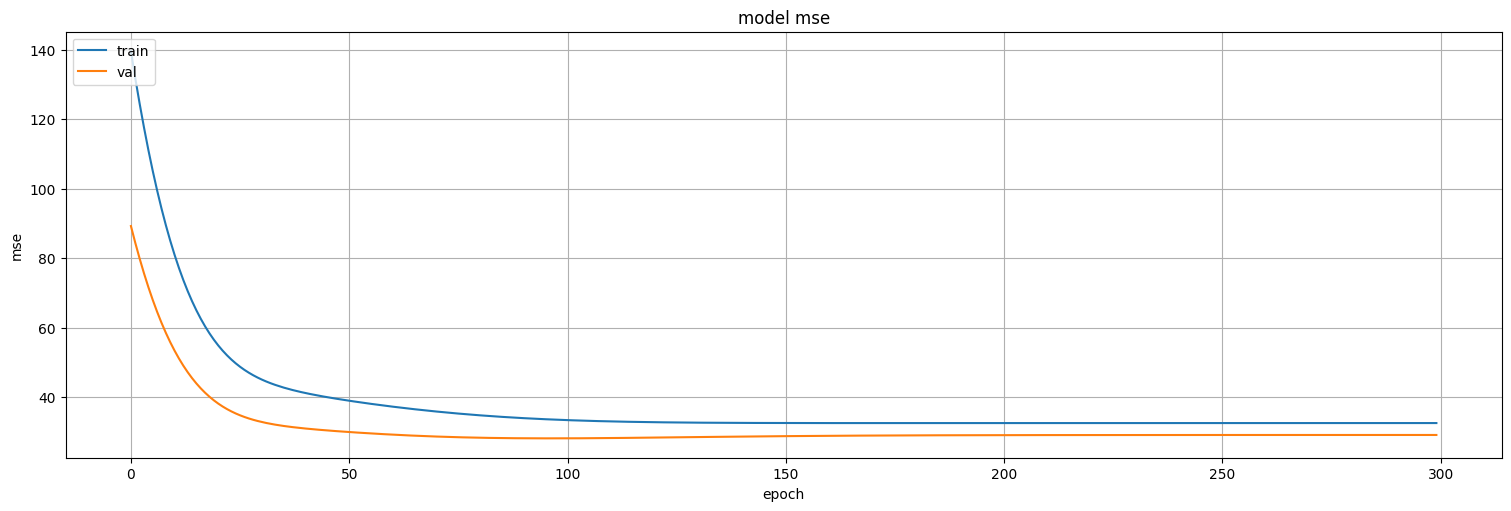
pred = model.predict(dataset)
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
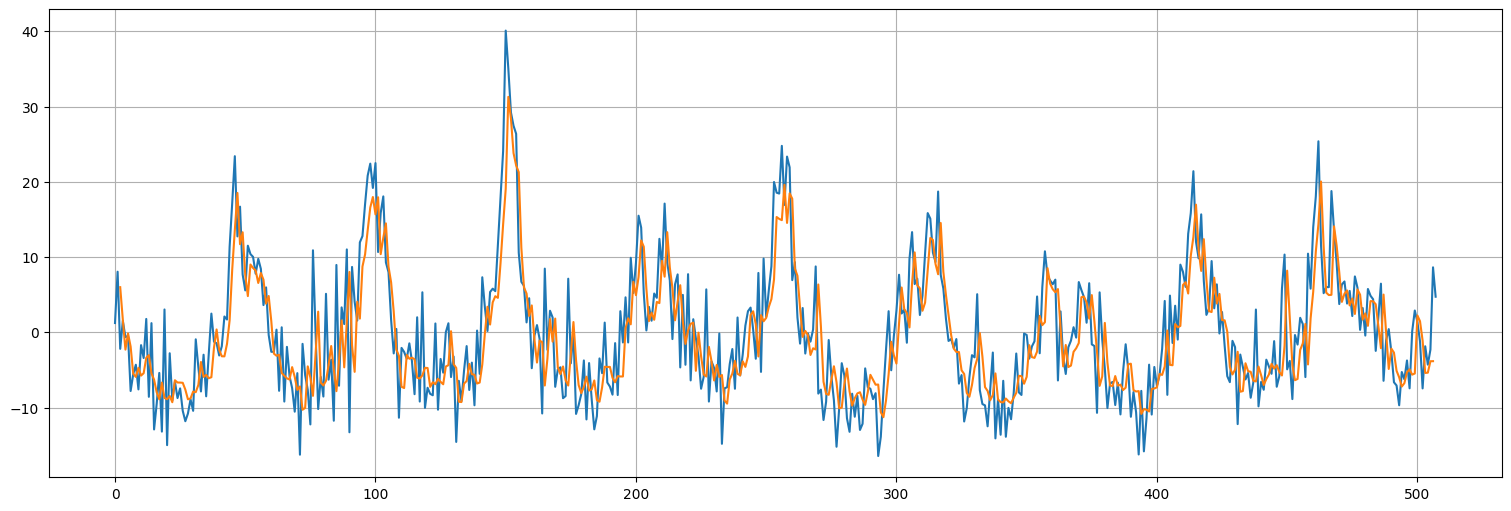
plt.plot(x.values)
plt.plot(range(window,x.size-window+1),pred);
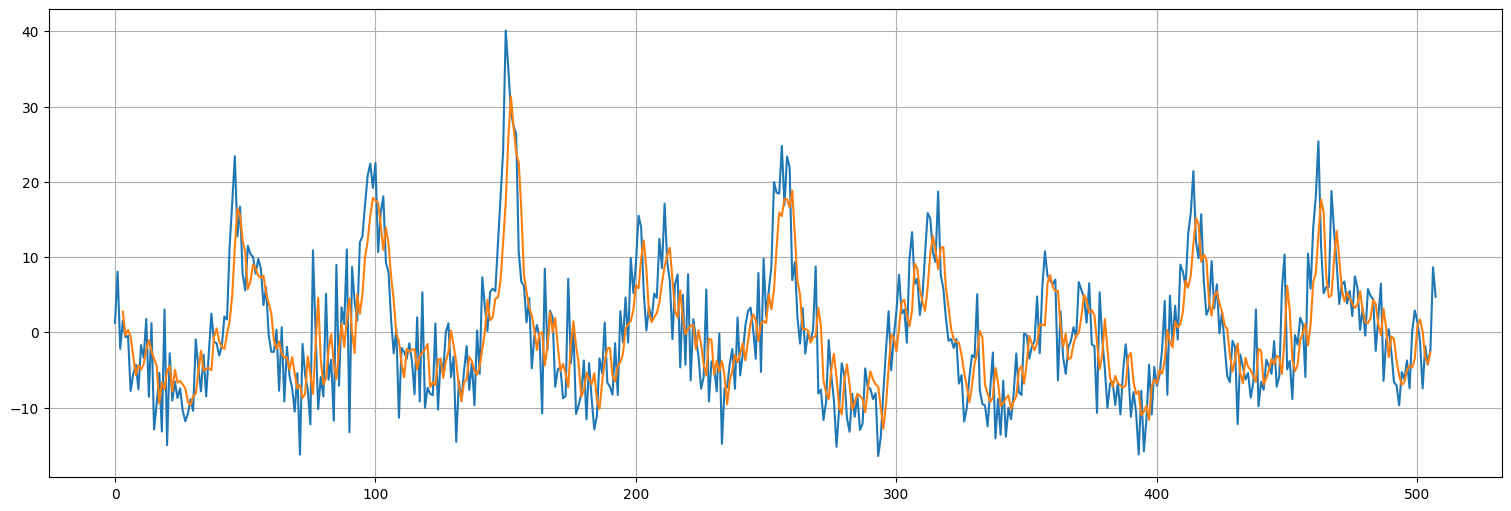
model.get_weights()
[array([[0.0187821 ],
[0.45386124],
[0.36643973]], dtype=float32),
array([-0.10907853], dtype=float32)]
from statsmodels.tsa.api import ARIMA
x_train=x.iloc[:406]
arima = ARIMA(x_train,order=(window,0,0), trend='c').fit()
arima.summary()
| Dep. Variable: | y | No. Observations: | 406 |
|---|---|---|---|
| Model: | ARIMA(3, 0, 0) | Log Likelihood | -1283.337 |
| Date: | Wed, 12 Jun 2024 | AIC | 2576.675 |
| Time: | 20:11:50 | BIC | 2596.707 |
| Sample: | 01-04-1970 | HQIC | 2584.603 |
| - 10-16-1977 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -0.3526 | 1.865 | -0.189 | 0.850 | -4.007 | 3.302 |
| ar.L1 | 0.3794 | 0.045 | 8.471 | 0.000 | 0.292 | 0.467 |
| ar.L2 | 0.4591 | 0.050 | 9.098 | 0.000 | 0.360 | 0.558 |
| ar.L3 | 0.0041 | 0.052 | 0.079 | 0.937 | -0.098 | 0.106 |
| sigma2 | 32.4955 | 2.127 | 15.275 | 0.000 | 28.326 | 36.665 |
| Ljung-Box (L1) (Q): | 0.00 | Jarque-Bera (JB): | 8.96 |
|---|---|---|---|
| Prob(Q): | 0.97 | Prob(JB): | 0.01 |
| Heteroskedasticity (H): | 0.73 | Skew: | 0.30 |
| Prob(H) (two-sided): | 0.07 | Kurtosis: | 3.40 |
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
arima.mse
32.52697246853836
model.evaluate(train)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 486us/step - loss: 33.2681 - mse: 33.2681
[32.54787826538086, 32.54787826538086]
Modelo 2: múltiples capas densas¶
Agreguemos algunas capas para darle no linealidad al modelo. Usamos como función de activación relu, es decir \(a(x)=\max\{x,0\}\).
model2 = keras.Sequential([
keras.Input(shape=(window,)),
keras.layers.Dense(units=32, activation='relu'),
keras.layers.Dense(units=1)
])
model2.summary()
Model: "sequential_5"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_8 (Dense) │ (None, 32) │ 128 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_9 (Dense) │ (None, 1) │ 33 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 161 (644.00 B)
Trainable params: 161 (644.00 B)
Non-trainable params: 0 (0.00 B)
model2.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model2.fit(
train,
epochs=200,
verbose=False,
validation_data=test
)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
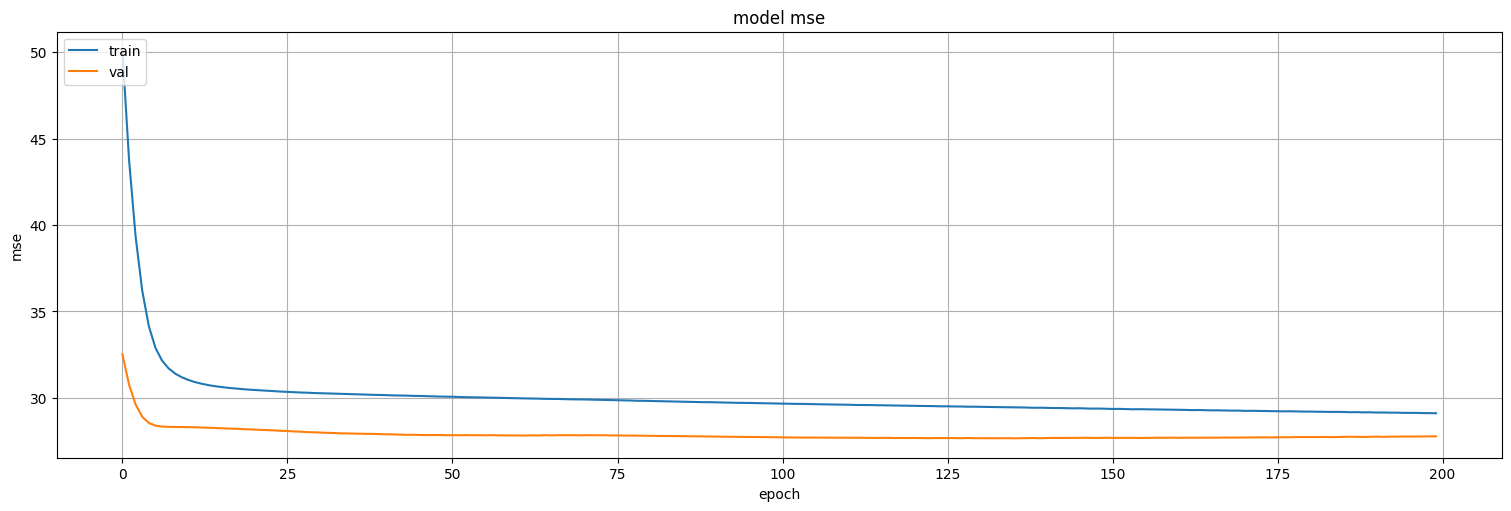
model.evaluate(test)
model2.evaluate(test)
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 807us/step - loss: 30.3401 - mse: 30.3401
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 28.1381 - mse: 28.1381
[27.77257537841797, 27.77257537841797]
pred = model2.predict(dataset)
32/32 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
plt.plot(x.values)
plt.plot(range(window,x.size-window+1),pred);
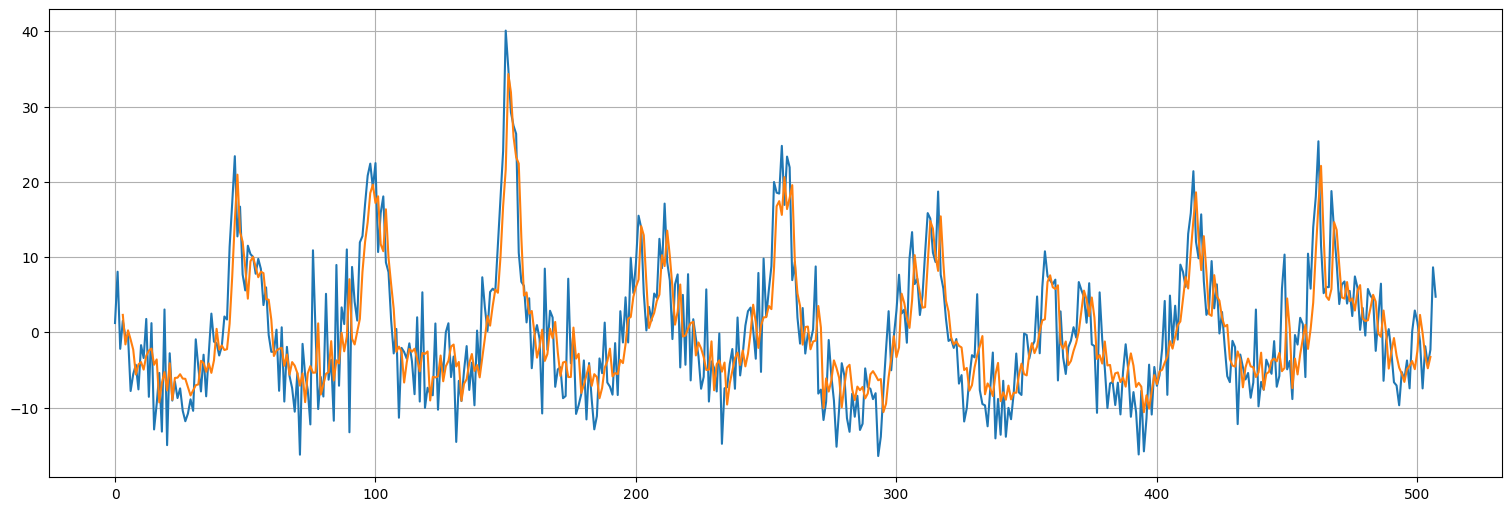
Modelo 3: agregando características¶
Agreguemos ahora al conjunto de entrenamiento algunas funciones del tiempo. Por ejemplo, la semana del año:
Preprocesamiento¶
window = 3 #lags a mirar
n = x.size-window
week = [x.index[i].weekofyear for i in range(0,n)]
#cost = np.cos(2*np.pi*freq*t)
#sint = np.sin(2*np.pi*freq*t)
features = 2
input_data = np.stack([x.values[:-window],week], axis=1)
targets = x.values[window:]
dataset = keras.utils.timeseries_dataset_from_array(input_data, targets, sequence_length=window, batch_size=4)
train, test = keras.utils.split_dataset(dataset,0.8)
2024-06-12 20:23:05.802270: W tensorflow/core/framework/local_rendezvous.cc:404] Local rendezvous is aborting with status: OUT_OF_RANGE: End of sequence
Ajuste¶
model3 = keras.Sequential([
keras.Input(shape=(window,features)),
keras.layers.Reshape((1,window*features)),
tf.keras.layers.Dense(units=1)
])
model3.summary()
Model: "sequential_7"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ reshape_1 (Reshape) │ (None, 1, 6) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_11 (Dense) │ (None, 1, 1) │ 7 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 7 (28.00 B)
Trainable params: 7 (28.00 B)
Non-trainable params: 0 (0.00 B)
model3.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model3.fit(
train,
epochs=200,
verbose=False,
validation_data=test
)
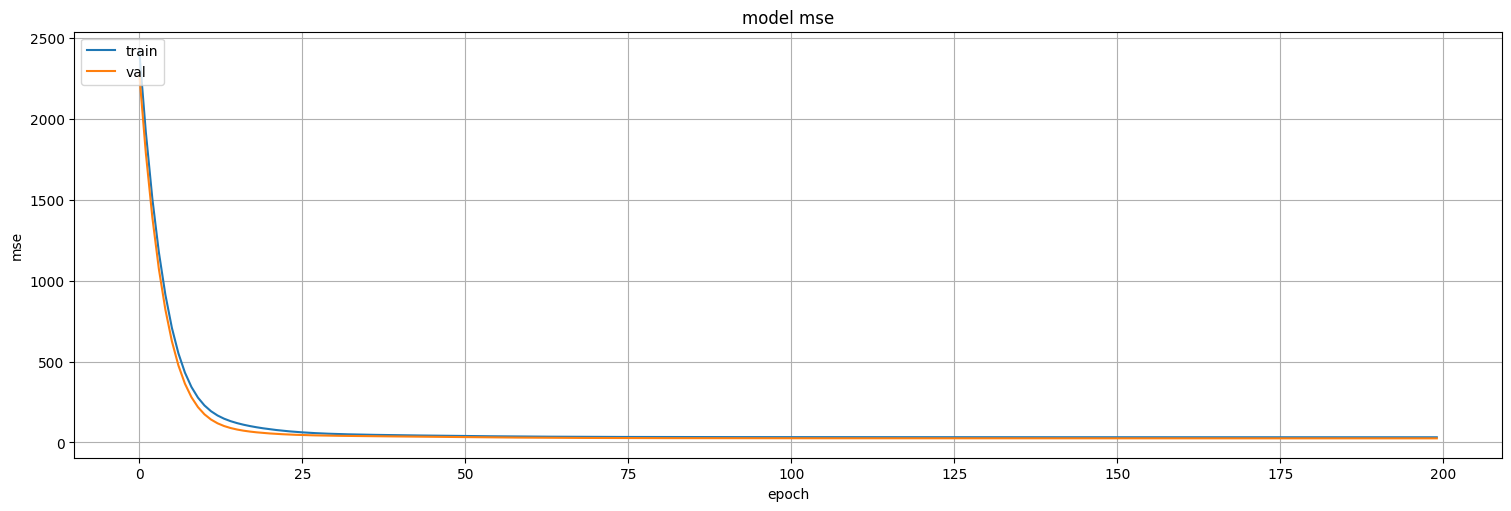
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
model3.evaluate(test)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 491us/step - loss: 25.1285 - mse: 25.1285
[25.332748413085938, 25.332748413085938]
pred = model3.predict(dataset)
pred = np.reshape(pred,(len(x)-2*window+1,1))
126/126 ━━━━━━━━━━━━━━━━━━━━ 0s 764us/step
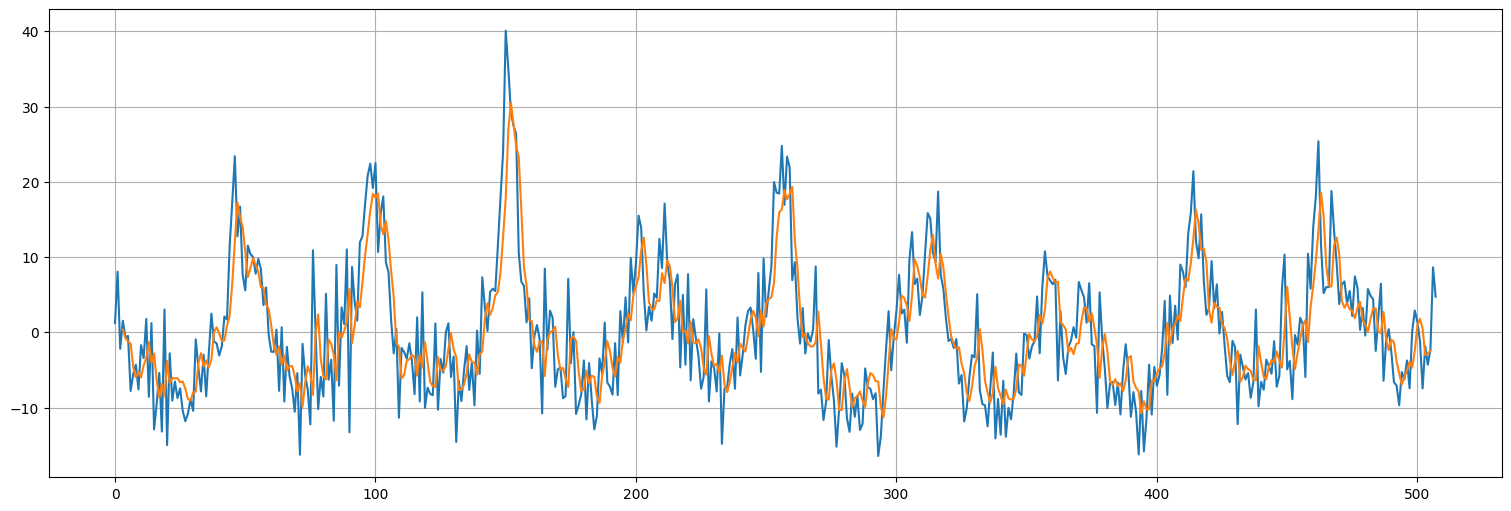
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred);
Modelo 4: características y capas¶
Agreguemos un par de capas densas intermedias
model4 = keras.Sequential([
keras.Input(shape=(window,features)),
keras.layers.Reshape((1,window*features)),
keras.layers.Dense(units=16,activation="relu"),
keras.layers.Dense(units=8,activation="relu"),
tf.keras.layers.Dense(units=1)
])
model4.summary()
Model: "sequential_13"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ reshape_7 (Reshape) │ (None, 1, 6) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_27 (Dense) │ (None, 1, 16) │ 112 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_28 (Dense) │ (None, 1, 8) │ 136 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_29 (Dense) │ (None, 1, 1) │ 9 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 257 (1.00 KB)
Trainable params: 257 (1.00 KB)
Non-trainable params: 0 (0.00 B)
model4.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model4.fit(
train,
epochs=50,
verbose=False,
validation_data=test
)
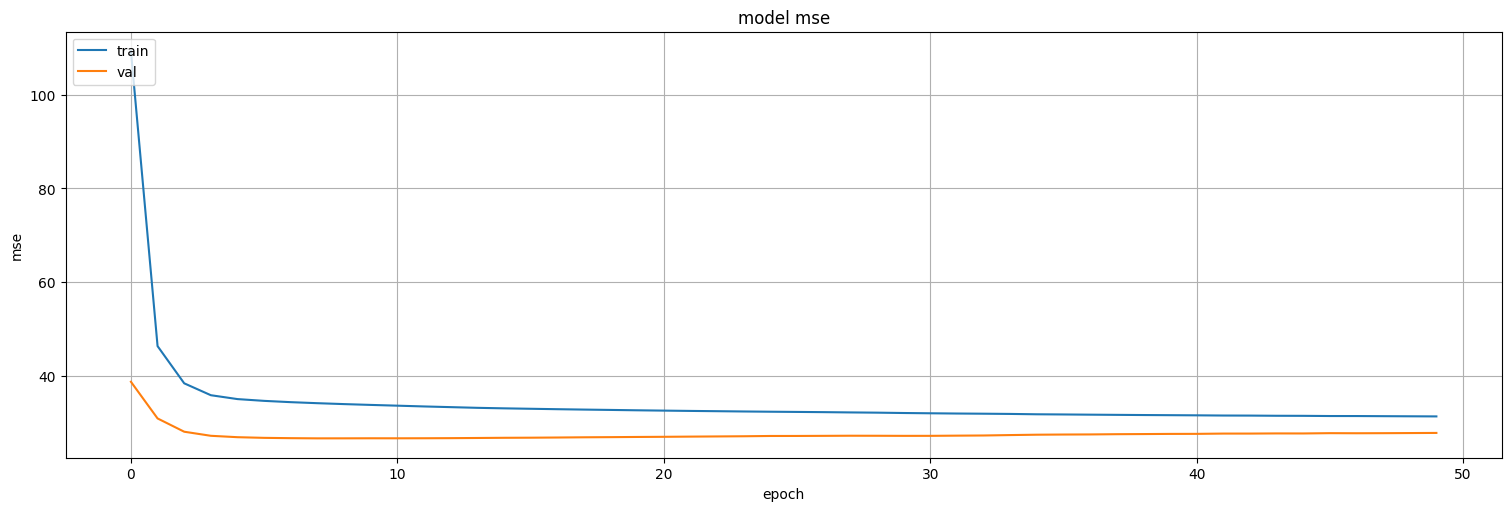
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
model4.evaluate(test)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 580us/step - loss: 27.8429 - mse: 27.8429
[27.725839614868164, 27.725839614868164]
pred = model4.predict(dataset)
pred = np.reshape(pred,(len(x)-2*window+1,1))
126/126 ━━━━━━━━━━━━━━━━━━━━ 0s 983us/step
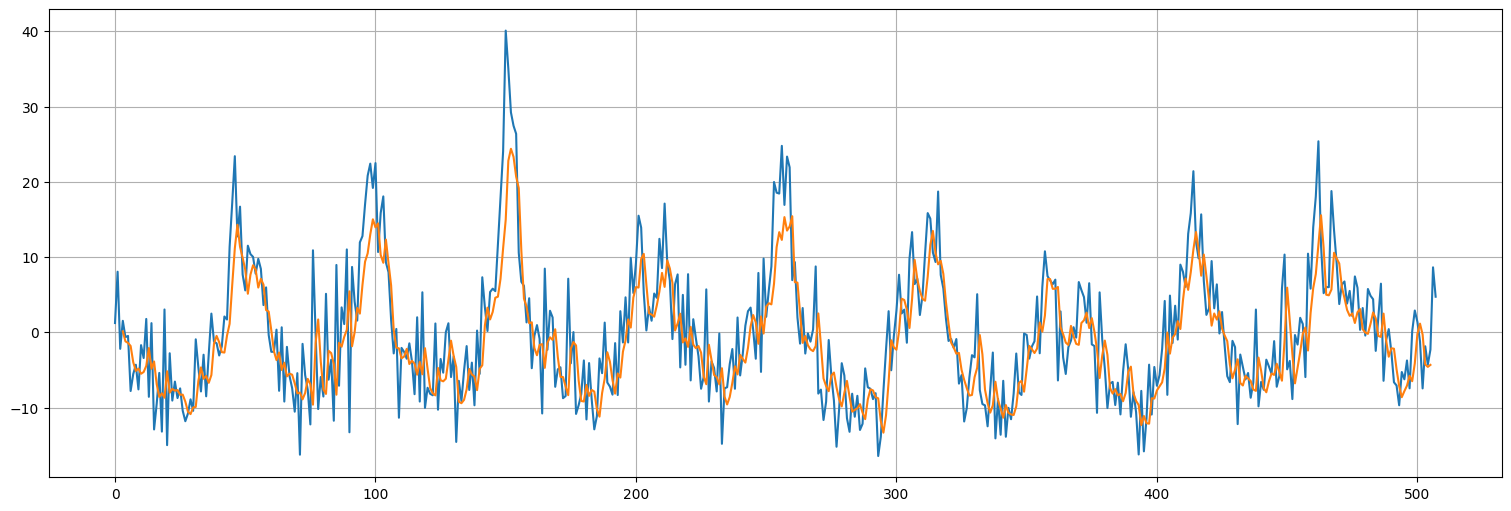
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred);
Modelo 5: Convolutional Neural Network¶
La idea de la capa convolucional o CNN es similar a la de los procesos autorregresivos y a lo que veníamos haciendo antes, solo que simplifica un poco la escritura del modelo. El de abajo es esencialmente el mismo modelo 4 pero usando CNNs.
Preprocesamiento¶
window = 3 #lags a mirar
n = x.size-window
week = [x.index[i].weekofyear for i in range(0,n)]
#cost = np.cos(2*np.pi*freq*t)
#sint = np.sin(2*np.pi*freq*t)
features = 2
input_data = np.stack([x.values[:-window],week], axis=1)
targets = x.values[window:]
dataset = keras.utils.timeseries_dataset_from_array(input_data, targets, sequence_length=window, batch_size=4)
train, test = keras.utils.split_dataset(dataset,0.8)
2024-06-12 20:33:07.797055: W tensorflow/core/framework/local_rendezvous.cc:404] Local rendezvous is aborting with status: OUT_OF_RANGE: End of sequence
model5 = keras.Sequential([
keras.Input(shape=(1,features)),
keras.layers.Conv1D(filters=16, kernel_size=window, activation="relu", padding="causal"),
keras.layers.Dense(units=8,activation="relu"),
tf.keras.layers.Dense(units=1)
])
model5.summary()
Model: "sequential_14"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ conv1d (Conv1D) │ (None, 1, 16) │ 112 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_30 (Dense) │ (None, 1, 8) │ 136 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_31 (Dense) │ (None, 1, 1) │ 9 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 257 (1.00 KB)
Trainable params: 257 (1.00 KB)
Non-trainable params: 0 (0.00 B)
model5.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model5.fit(
train,
epochs=200,
verbose=False,
validation_data=test,
callbacks=keras.callbacks.EarlyStopping(monitor='val_loss', patience=3)
)
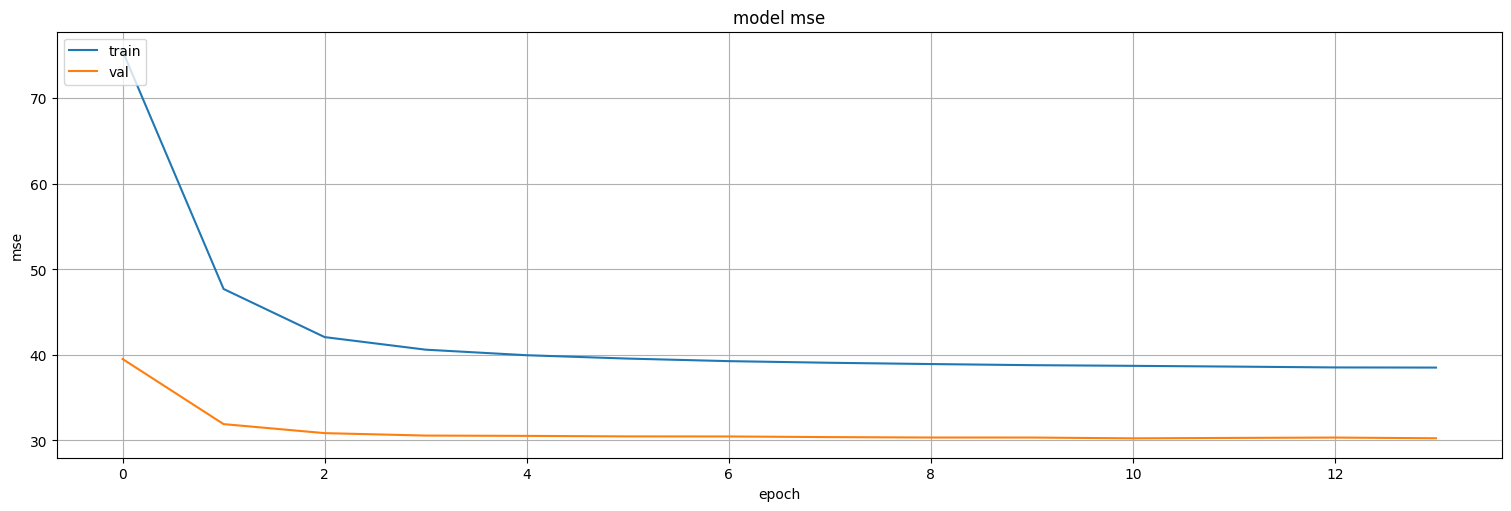
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
model5.evaluate(test)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 485us/step - loss: 31.1125 - mse: 31.1125
[30.25593376159668, 30.25593376159668]
pred = model5.predict(dataset)
pred.shape
126/126 ━━━━━━━━━━━━━━━━━━━━ 0s 915us/step
(503, 3, 1)
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred[:,2,0]);
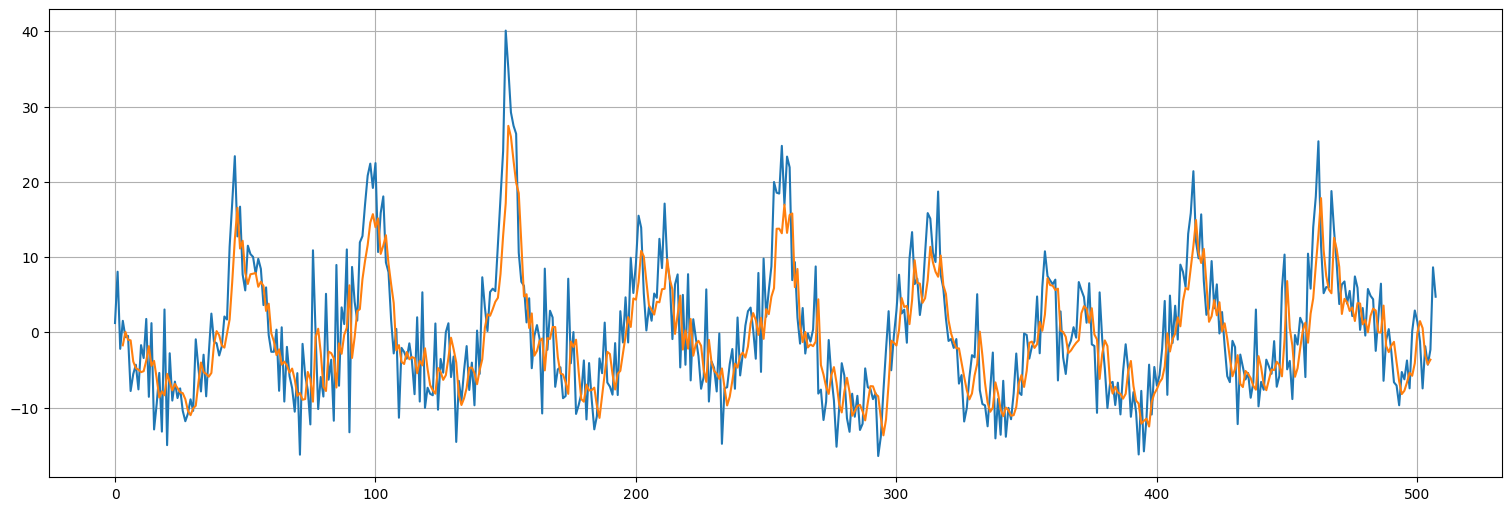
Múltiples capas convolucionales con dilation¶
window = 2 #lags a mirar
n = x.size-window
input_data = x.values[:-window]
targets = x.values[window:]
dataset = keras.utils.timeseries_dataset_from_array(input_data, targets, sequence_length=window, batch_size=1)
train, test = keras.utils.split_dataset(dataset,0.8)
2024-06-12 20:40:41.812653: W tensorflow/core/framework/local_rendezvous.cc:404] Local rendezvous is aborting with status: OUT_OF_RANGE: End of sequence
model5 = keras.Sequential([
keras.Input(shape=(1,1)),
keras.layers.Conv1D(filters=16, kernel_size=window, activation="relu", padding="causal"),
keras.layers.Conv1D(filters=8, kernel_size=2, dilation_rate = 2*window, activation="relu", padding="causal"),
keras.layers.Conv1D(filters=4, kernel_size=2, dilation_rate = 4*window, activation="relu", padding="causal"),
tf.keras.layers.Dense(units=1)
])
model5.summary()
Model: "sequential_15"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ conv1d_1 (Conv1D) │ (None, 1, 16) │ 48 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv1d_2 (Conv1D) │ (None, 1, 8) │ 264 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv1d_3 (Conv1D) │ (None, 1, 4) │ 68 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_32 (Dense) │ (None, 1, 1) │ 5 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 385 (1.50 KB)
Trainable params: 385 (1.50 KB)
Non-trainable params: 0 (0.00 B)
model5.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model5.fit(
train,
epochs=200,
verbose=False,
validation_data=test,
callbacks=keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
)
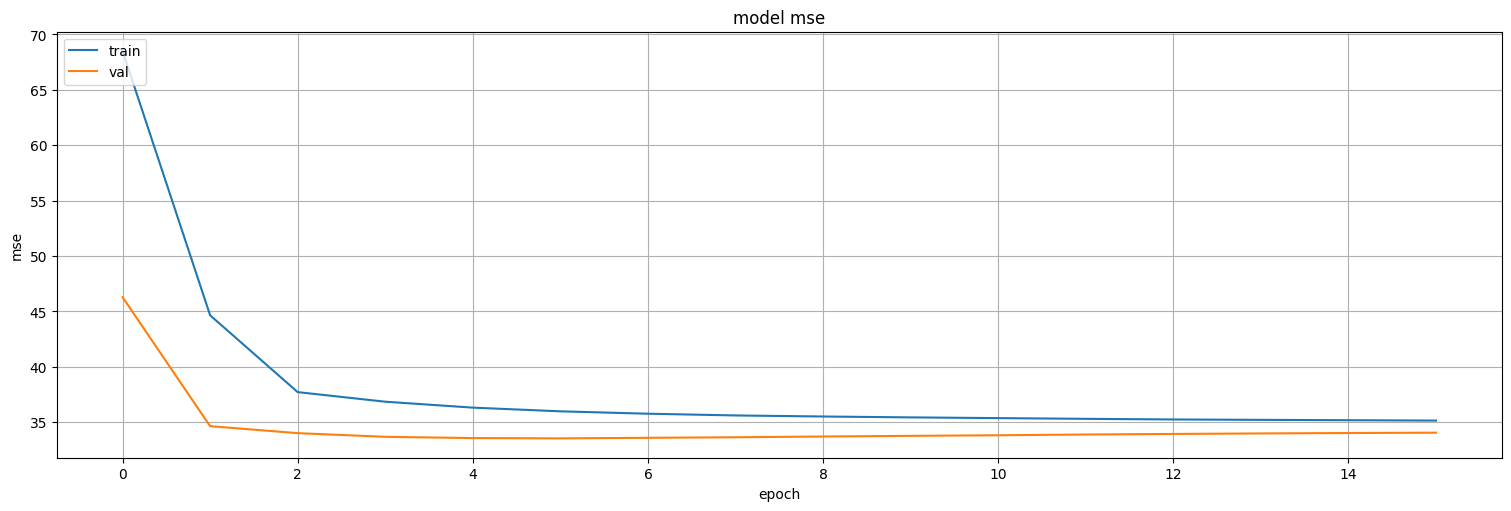
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
model5.evaluate(test)
101/101 ━━━━━━━━━━━━━━━━━━━━ 0s 568us/step - loss: 32.8034 - mse: 32.8034
[34.05792236328125, 34.05792236328125]
pred = model5.predict(dataset)
pred.shape
505/505 ━━━━━━━━━━━━━━━━━━━━ 0s 671us/step
(505, 2, 1)
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred[:,window-1,0]);
Recurrent Neural Networks¶
Estas redes permiten “guardar estado” y en algún sentido son la generalización no lineal del Dynamic Linear model que ya vimos. Permiten en algún sentido agregar memoria.
El proceso en una capa RNN es:
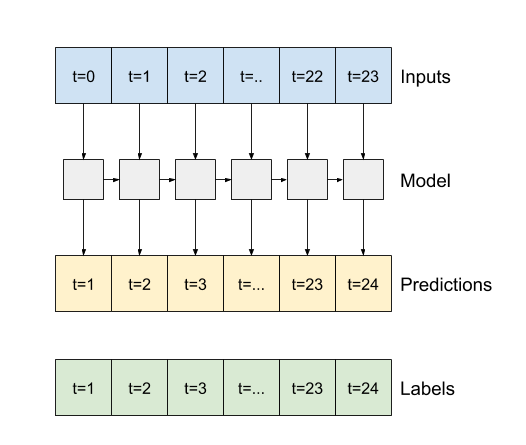
Modelo 6: Simple RNN¶
La red recurrente simple tiene “memoria corta” y presenta problemas de ajuste (“vanishing and exploding gradients”) cuando uno hace el algoritmo de Backpropagation adaptado a las mismas.
window = 3 #lags a mirar
n = x.size-window
input_data = x.values[:-window]
targets = x.values[window:]
dataset = keras.utils.timeseries_dataset_from_array(input_data, targets, sequence_length=window, batch_size=1)
train, test = keras.utils.split_dataset(dataset,0.8)
2024-06-12 20:46:40.197622: W tensorflow/core/framework/local_rendezvous.cc:404] Local rendezvous is aborting with status: OUT_OF_RANGE: End of sequence
model6 = keras.Sequential([
keras.Input(shape=(window,1)),
keras.layers.Reshape((1,window)), #necesario porque los valores anteriores de la serie son considerados "features" en la RNN.
keras.layers.SimpleRNN(units=8, activation="relu"),
tf.keras.layers.Dense(units=1)
])
model6.summary()
Model: "sequential_16"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ reshape_8 (Reshape) │ (None, 1, 3) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ simple_rnn (SimpleRNN) │ (None, 8) │ 96 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_33 (Dense) │ (None, 1) │ 9 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 105 (420.00 B)
Trainable params: 105 (420.00 B)
Non-trainable params: 0 (0.00 B)
model6.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model6.fit(
train,
epochs=200,
verbose=False,
validation_data=test,
callbacks=keras.callbacks.EarlyStopping(monitor='val_loss', patience=3)
)
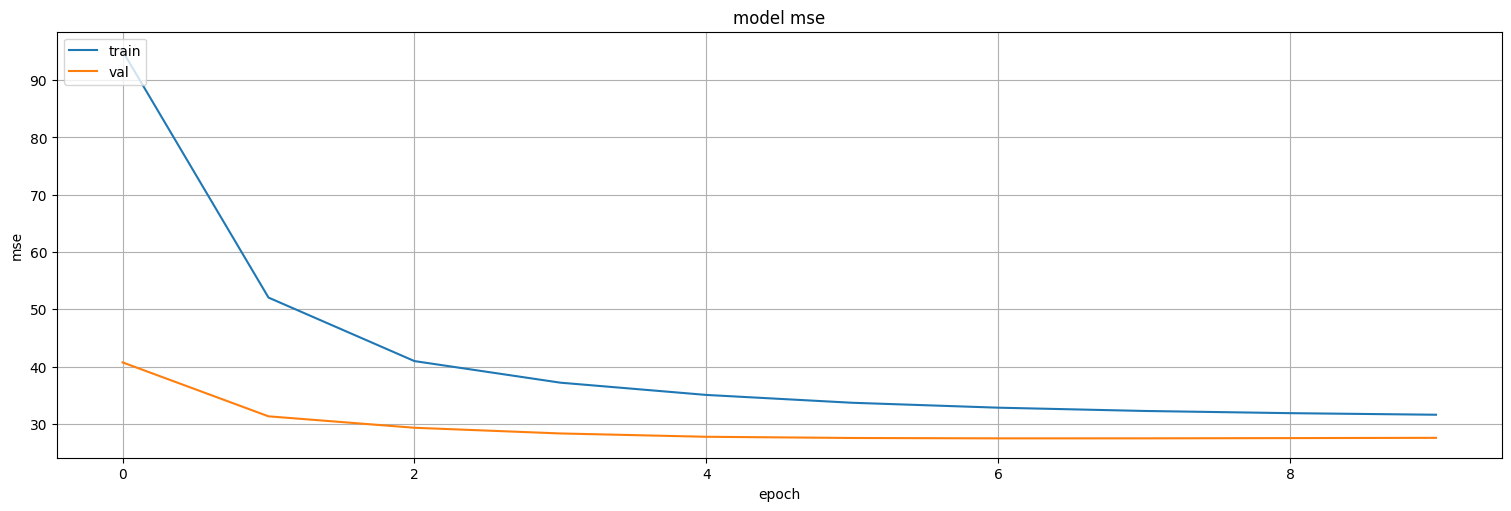
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
model6.evaluate(test)
101/101 ━━━━━━━━━━━━━━━━━━━━ 0s 479us/step - loss: 27.3341 - mse: 27.3341
[27.543731689453125, 27.543731689453125]
pred = model6.predict(dataset)
pred.shape
503/503 ━━━━━━━━━━━━━━━━━━━━ 0s 649us/step
(503, 1)
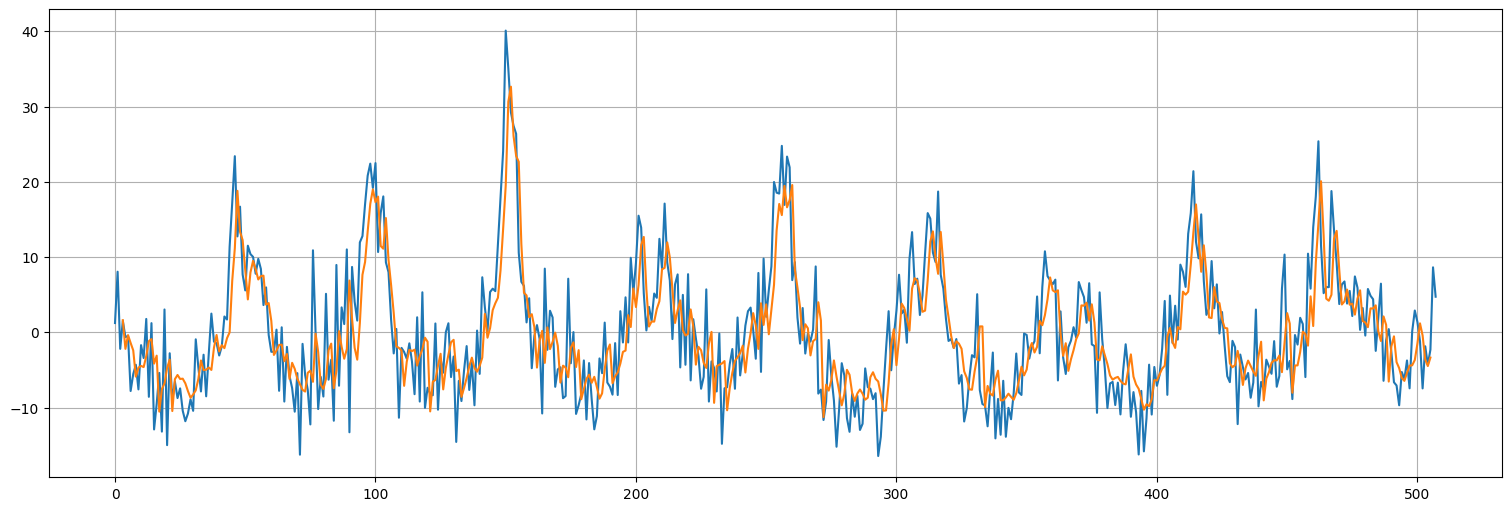
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred);
RNN con features¶
window = 3 #lags a mirar
n = x.size-window
week = [x.index[i].weekofyear for i in range(0,n)]
features = 2
input_data = np.stack([x.values[:-window],week], axis=1)
targets = x.values[window:]
dataset = keras.utils.timeseries_dataset_from_array(input_data, targets, sequence_length=window, batch_size=4)
train, test = keras.utils.split_dataset(dataset,0.8)
2024-06-12 20:50:29.275157: W tensorflow/core/framework/local_rendezvous.cc:404] Local rendezvous is aborting with status: OUT_OF_RANGE: End of sequence
model7 = keras.Sequential([
keras.Input(shape=(window,features)),
keras.layers.Reshape((1,window*features)), #necesario porque los valores anteriores de la serie son considerados "features" en la RNN.
keras.layers.SimpleRNN(units=8, activation="relu"),
tf.keras.layers.Dense(units=1)
])
model7.summary()
Model: "sequential_18"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ reshape_10 (Reshape) │ (None, 1, 6) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ simple_rnn_2 (SimpleRNN) │ (None, 8) │ 120 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_35 (Dense) │ (None, 1) │ 9 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 129 (516.00 B)
Trainable params: 129 (516.00 B)
Non-trainable params: 0 (0.00 B)
model7.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model7.fit(
train,
epochs=200,
verbose=False,
validation_data=test,
callbacks=keras.callbacks.EarlyStopping(monitor='val_loss', patience=3)
)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
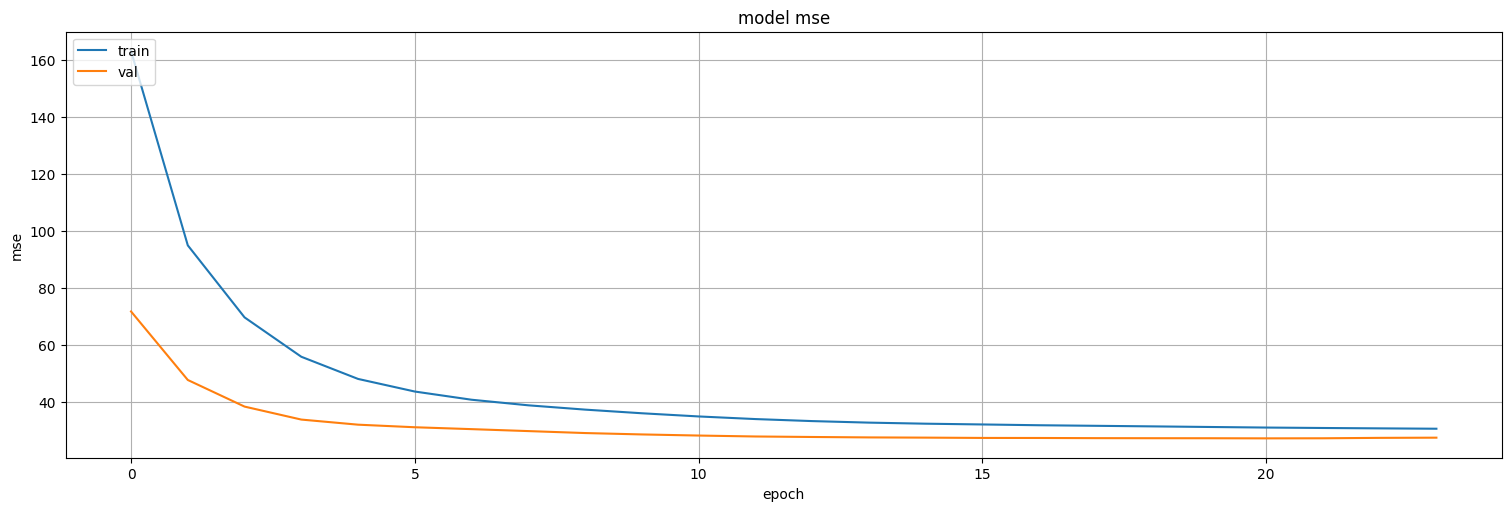
model7.evaluate(test)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 646us/step - loss: 26.6596 - mse: 26.6596
[27.382709503173828, 27.382709503173828]
pred = model7.predict(dataset)
pred.shape
126/126 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
(503, 1)
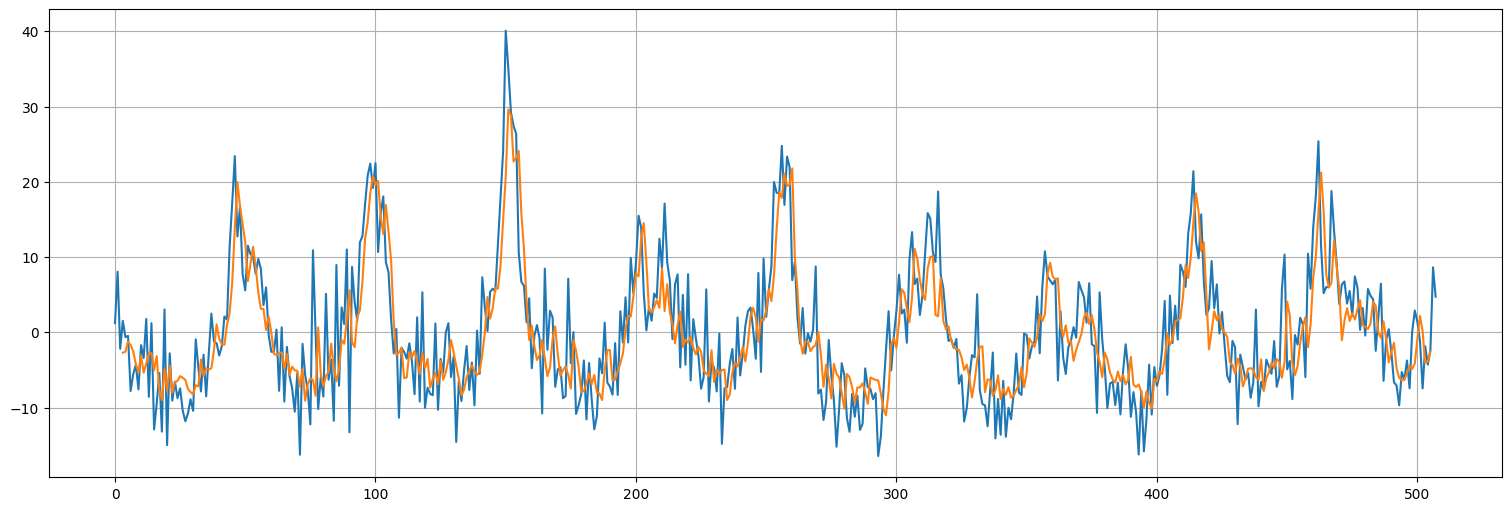
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred);
Modelo 8: LSTM¶
La red recurrente LSTM funciona igual que la red RNN en principio, pero tiene más “gates” y parámetros internos para permitir guardar más estado interno. Estas redes son muy usadas para series temporales.
model8 = keras.Sequential([
keras.Input(shape=(window,features)),
keras.layers.Reshape((1,window*features)), #necesario porque los valores anteriores de la serie son considerados "features" en la RNN.
keras.layers.LSTM(units=8, activation="relu"),
tf.keras.layers.Dense(units=1)
])
model8.summary()
Model: "sequential_22"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ reshape_14 (Reshape) │ (None, 1, 6) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_3 (LSTM) │ (None, 8) │ 480 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_39 (Dense) │ (None, 1) │ 9 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 489 (1.91 KB)
Trainable params: 489 (1.91 KB)
Non-trainable params: 0 (0.00 B)
model8.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model8.fit(
train,
epochs=200,
verbose=False,
validation_data=test,
callbacks=keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
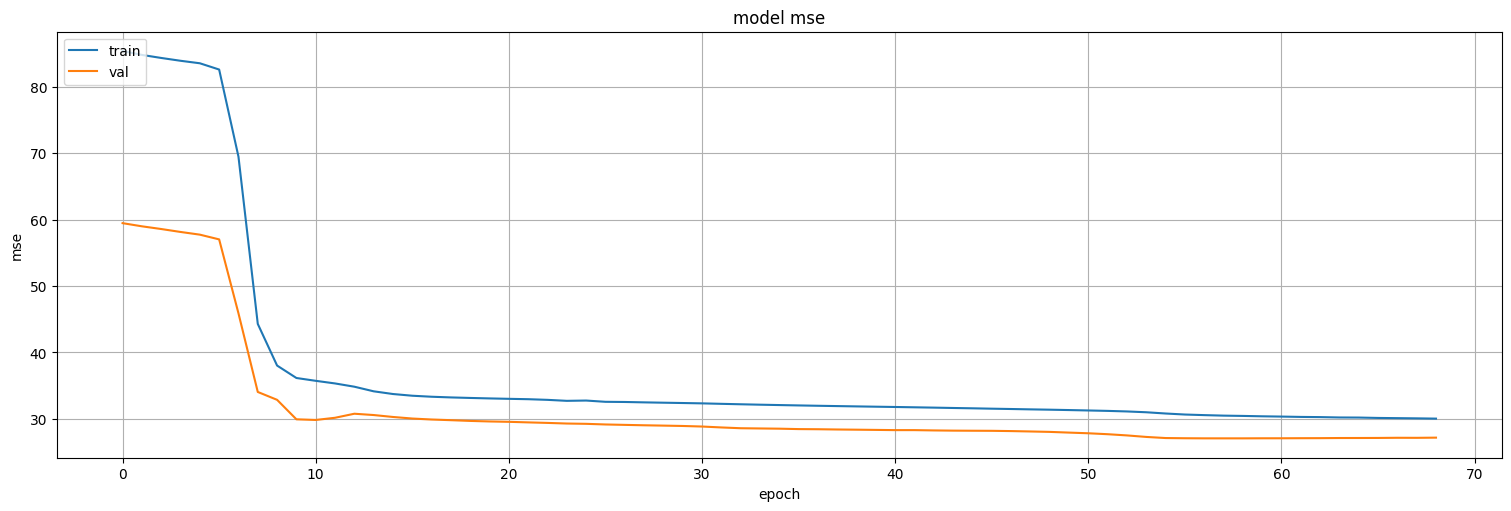
model8.evaluate(test)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 595us/step - loss: 26.3951 - mse: 26.3951
[27.157976150512695, 27.157976150512695]
pred = model8.predict(dataset)
pred.shape
126/126 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
(503, 1)
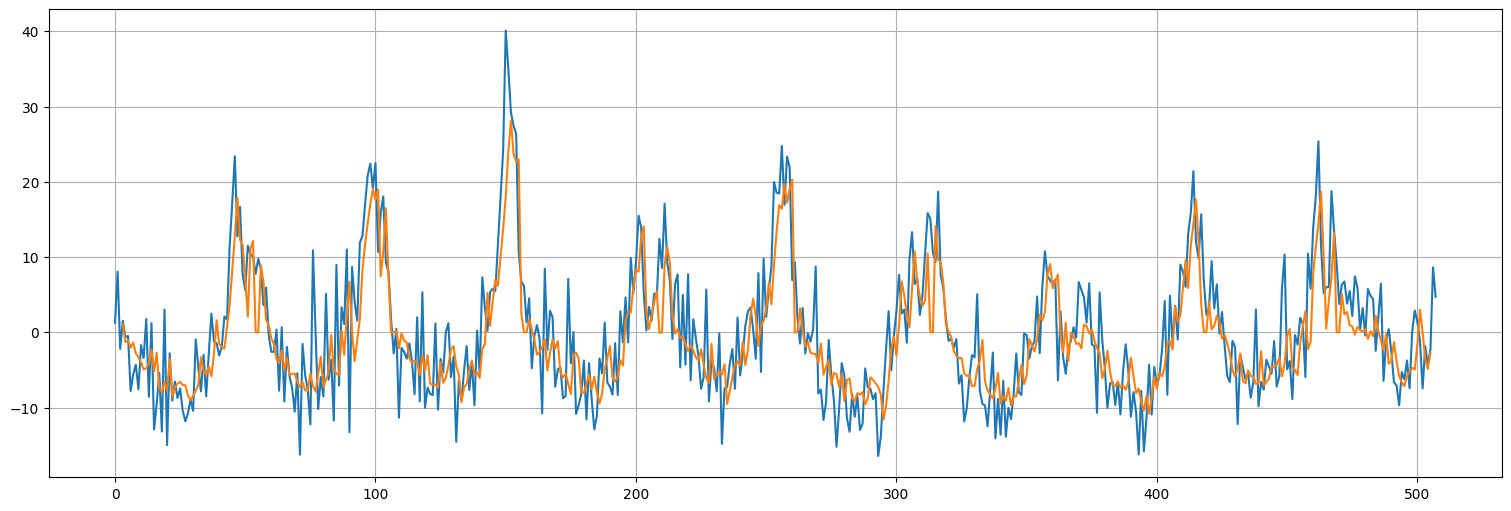
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred);
Modelo 8: LSTM + capas¶
Agreguemos alguna capa densa más.
model9 = keras.Sequential([
keras.Input(shape=(window,features)),
keras.layers.Reshape((1,window*features)), #necesario porque los valores anteriores de la serie son considerados "features" en la RNN.
keras.layers.Dense(units=8),
keras.layers.LSTM(units=8, activation="relu"),
keras.layers.Dense(units=8, activation="relu"),
keras.layers.Dense(units=1)
])
model9.summary()
Model: "sequential_23"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ reshape_15 (Reshape) │ (None, 1, 6) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_40 (Dense) │ (None, 1, 8) │ 56 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ lstm_4 (LSTM) │ (None, 8) │ 544 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_41 (Dense) │ (None, 8) │ 72 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_42 (Dense) │ (None, 1) │ 9 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 681 (2.66 KB)
Trainable params: 681 (2.66 KB)
Non-trainable params: 0 (0.00 B)
model9.compile(loss="mse",
optimizer = "adam",
metrics = ["mse"])
history = model9.fit(
train,
epochs=200,
verbose=False,
validation_data=test,
callbacks=keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model mse')
plt.ylabel('mse')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
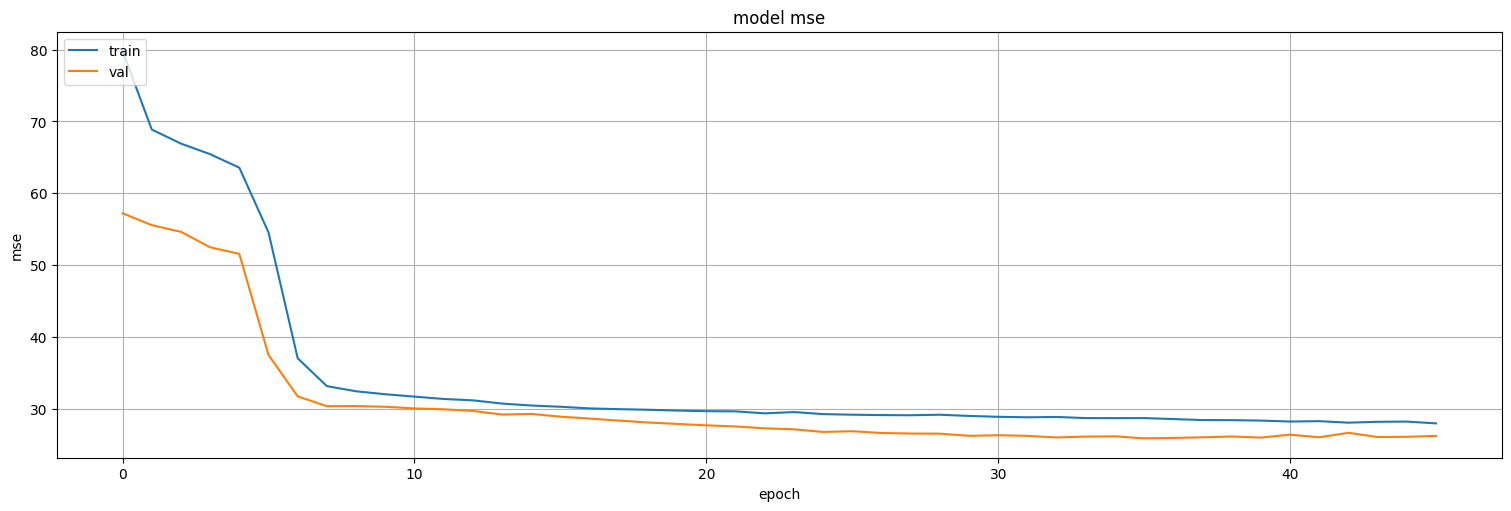
model9.evaluate(test)
26/26 ━━━━━━━━━━━━━━━━━━━━ 0s 904us/step - loss: 24.9205 - mse: 24.9205
[26.245861053466797, 26.245861053466797]
pred = model9.predict(dataset)
pred.shape
126/126 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
(503, 1)
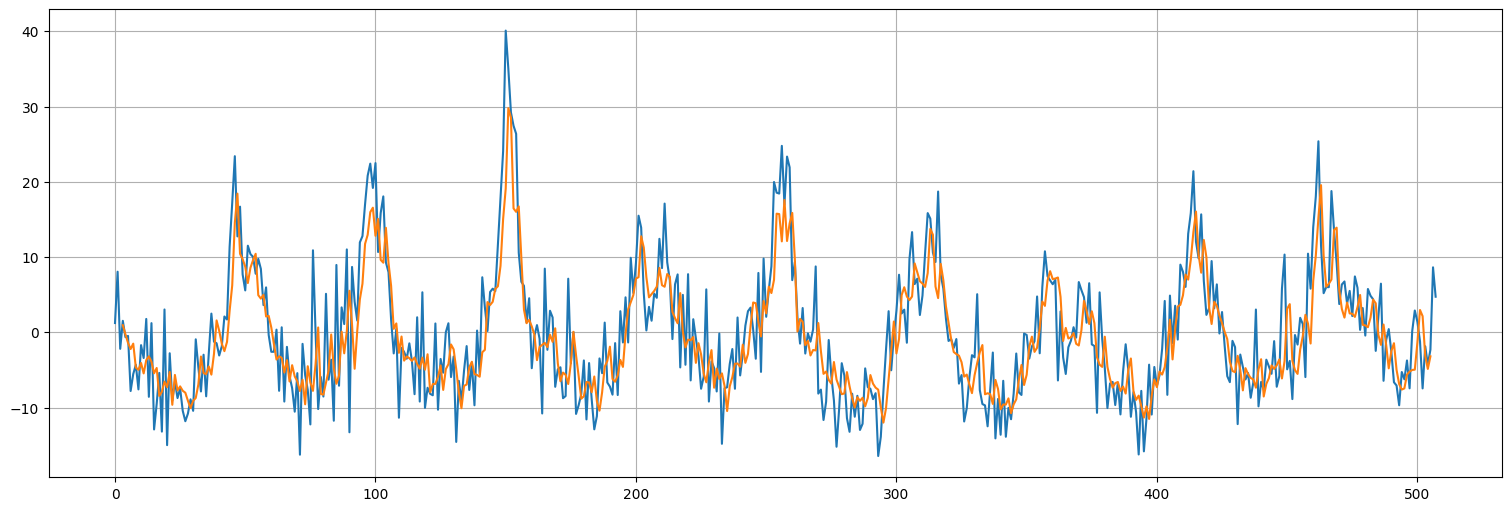
plt.plot(x.values)
plt.plot(range(window,len(x)-window+1),pred);
Conclusiones¶
El problema de predicción en series temporales puede transformarse en un problema de regresión sobre:
Los propios valores anteriores de la serie.
Otras funciones del tiempo.
Otras variables exógenas.
Las redes convolucionales son una versión no lineal de los modelos tipo ARMA vistos en clase. Se pueden superponer en capas y usar dilation para tener en cuenta dependencias largas
Las redes recurrentes son una versión no lineal de los modelos en espacio de estados vistos anteriormente.
Las redes LSTM son una versión de redes recurrentes que permite capturar dependencias largas.
Pero la conclusión más importante es que se necesitan muchos datos y ser muy cuidadoso en la validación para entrenar este tipo de modelos, y obtener resultados que mejoren lo visto anteriormente.