Modelos de Media Móvil, ARMA, y predicción.

Repaso:

Procesos autorregresivos

Recordemos primero la definición de proceso autorregresivo (de media 0):

Definición: un proceso \(\{x_t\}\) es autorregresivo de orden \(p\) si admite la representación

\[ x_t = \phi_1 x_{t-1} + \ldots + \phi_p x_{t-p} + w_t,\]

con \(w_t\) ruido blamco de varianza \(\sigma_w^2\).

Autocorrelación y autocorrelación parcial

En un proceso autorregresivo puro:

• La autocorrelación decae de forma exponencial como función del lag.

• La autocorrelación parcial se anula para lags mayores a \(p\).

Proceso de media móvil

Definición: un proceso \(\{x_t\}\) es una media móvil de orden \(q\) o \(MA(q)\) si verifica:

\[ x_t = w_t + \theta_1 w_{t-1} + \ldots + \theta_q w_{t-q},\]

donde hay \(q\) lags en la media móvil, \(\theta_1,\ldots,\theta_q\) son parámetros, \(\theta_q\neq0\) y \(\{w_t\}\) es ruido blanco (Gaussiano) de varianza \(\sigma^2_w\).

• Es el proceso dual del AR, donde el valor actual depende de valores pasados del ruido solamente, y no de la propia serie.

• El ruido blanco puede pensarse como una media móvil de orden \(0\).

• Si \(q>0\) el proceso es más suave que el ruido puro.

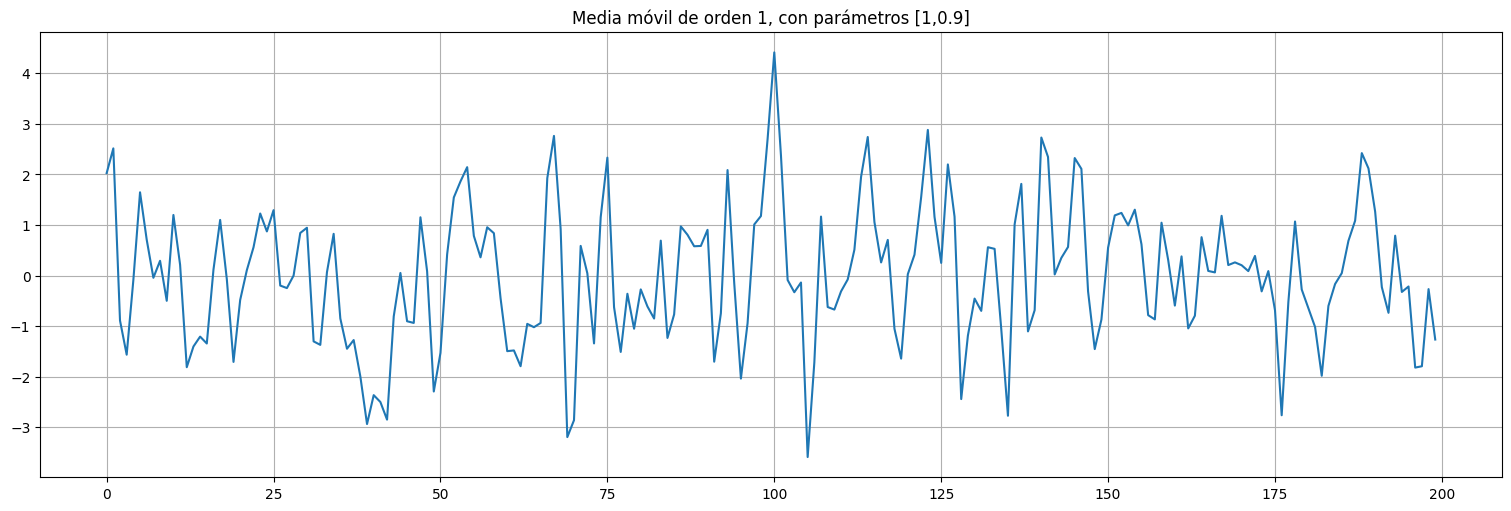
Ejemplo: MA(1)

Consideremos el proceso: $\(x_t = w_t + \theta w_{t-1}\)\( con \)w_t\( ruido blanco de varianza \)\sigma_w^2=1\( y \)\theta=0.9$.

## Ejemplo: media movil de orden 1
from statsmodels.tsa.arima_process import arma_generate_sample

theta = 0.9
#primer parámetro: coeficientes autorregresivos. Segundo parámetro: coeficientes de media móvil
#El tercer parámetro es la cantidad de muestras.
x=arma_generate_sample([1],[1,theta],200)
x=pd.Series(x)
x.plot();
plt.title(f"Media móvil de orden 1, con parámetros [1,{theta}]");

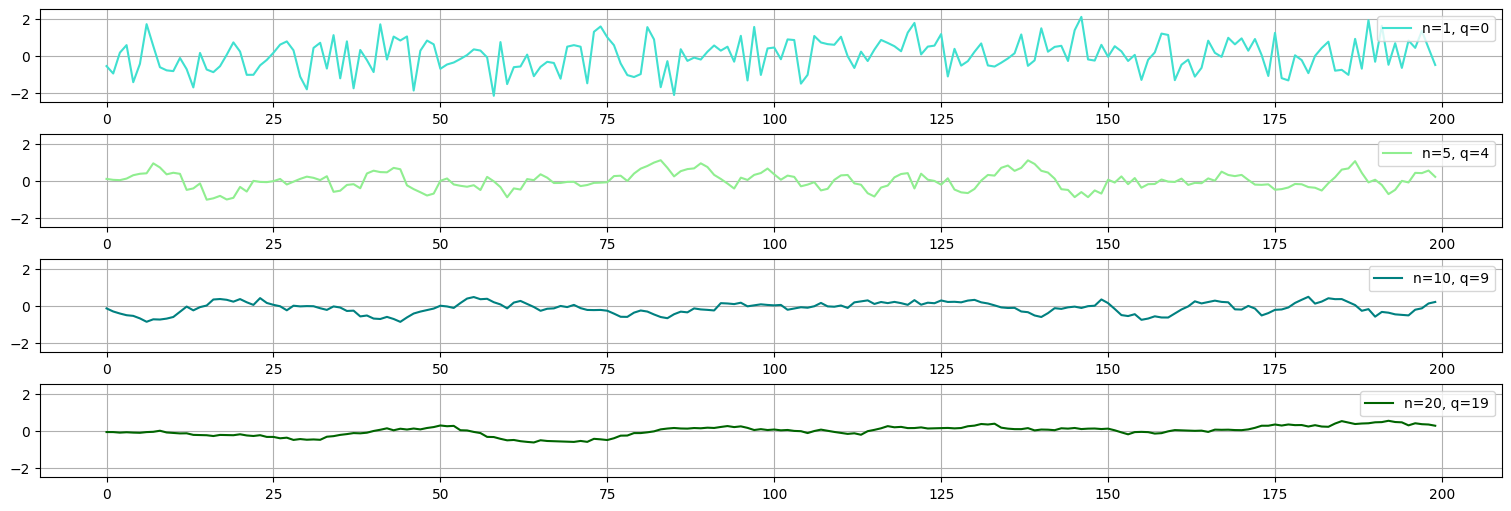
Ejemplo: media móvil de orden variable

Consideremos para cada \(n\) el proceso:

\[x_t = \frac{1}{n} \left(w_{t} + w_{t-1} + \ldots + w_{t-n+1}\right)\]

con \(w_t\) ruido blanco de varianza \(\sigma^2_w=1\).

Observar que este proceso es una media móvil de orden \(q = n-1\). Lo podemos escribir como:

\[n x_t = w_{t} + w_{t-1} + \ldots + w_{t-n+1}\]

Esta es la parametrización que le pasamos a arma_generate_sample:

## Ejemplo: media movil de orden variable
j=1
cmap = ['turquoise','lightgreen','teal','darkgreen']
for n in [1,5,10,20]:
    q=n-1
    x=arma_generate_sample([n],np.ones(n),200)
    x=pd.Series(x)
    plt.subplot(4,1,j)
    plt.plot(x,label=f"n={n}, q={q}", color=cmap[j-1]);
    plt.ylim(-2.5,2.5)
    plt.legend(loc='upper right');
    j=j+1

Ejemplo: media movil de orden 1

El proceso MA(1) está dado por

\[ x_t = w_t + \theta w_{t-1}.\]

Propiedades:

• \(E[x_t] = E[w_t] + \theta E[w_{t-1}] = 0\).

• \(E[x_t^2] = E[w_t^2] + 2\theta E[w_tw_{t-1}] + \theta^2 E[w_{t-1}^2] = (1+\theta^2)\sigma^2_w.\)

• \(E[x_t x_{t-1}] = E[(w_t + \theta w_{t-1})(w_{t-1} + \theta w_{t-2})] = \theta \sigma^2_w.\)

• \(E[x_t x_{t-h}] = 0\) si \(h>1\) porque los ruidos que participan no están correlacionados.

Resumiendo, la función de autocovarianza de un MA(1) tiene la forma:

\[\begin{split}\gamma(h) = \left\{\begin{array}{ll}(1+\theta^2)\sigma_w^2 & h=0\\ \theta\sigma_w^2 & h=\pm 1 \\ 0 & \text{en otro caso}\end{array}\right.\end{split}\]

La función de autocorrelación es entonces:

\[\begin{split}\rho(h) = \left\{\begin{array}{ll}1 & h=0\\ \frac{\theta}{1+\theta^2} & h=\pm 1 \\ 0 & \text{en otro caso}\end{array}\right.\end{split}\]

from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
theta=0.9
x=arma_generate_sample([1],[1,theta],500)
x=pd.Series(x)
plot_acf(x,bartlett_confint=False, label="Empirica");
plt.scatter(range(0,26),np.concatenate(([1],[theta/(1+theta**2)], np.zeros(24))), label="Teorica");
plt.legend();

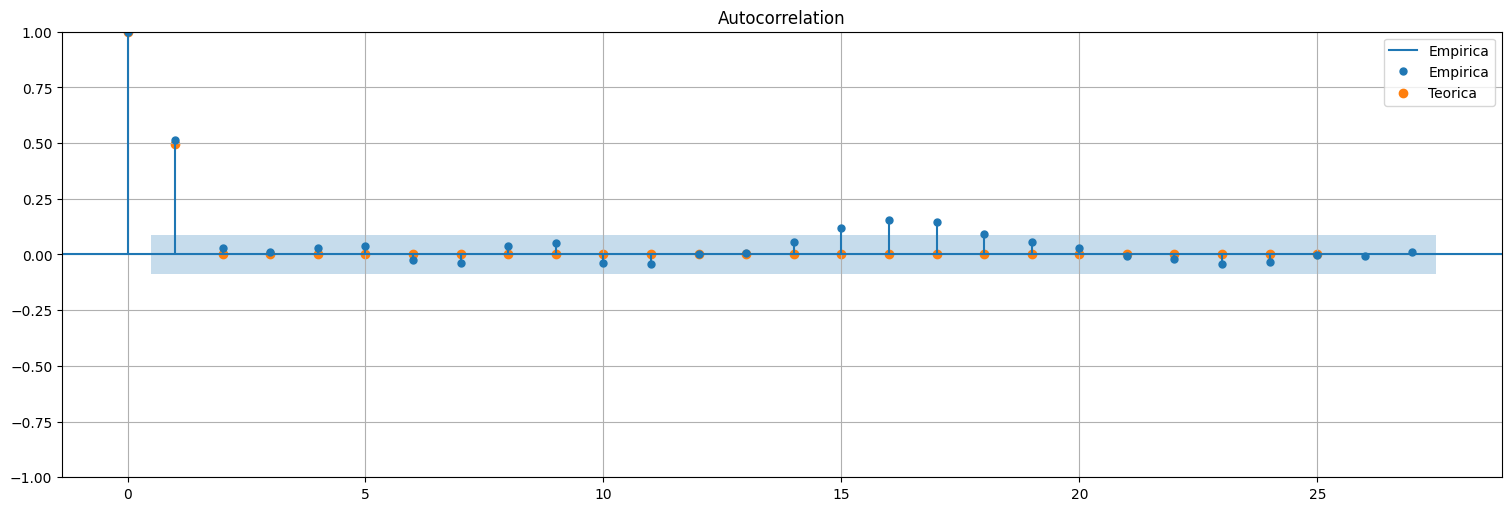
Observación:

La propiedad anterior es general, es decir, si \(x_t\) es un proceso \(MA(q)\) entonces la ACF de \(x_t\) es \(0\) para lags \(h>q\). Probemos con uno de orden \(q=5\) y coeficientes arbitrarios

x=arma_generate_sample([1],[1,.5,1,.5,1,.5],500)
x=pd.Series(x)
plot_acf(x,bartlett_confint=False);

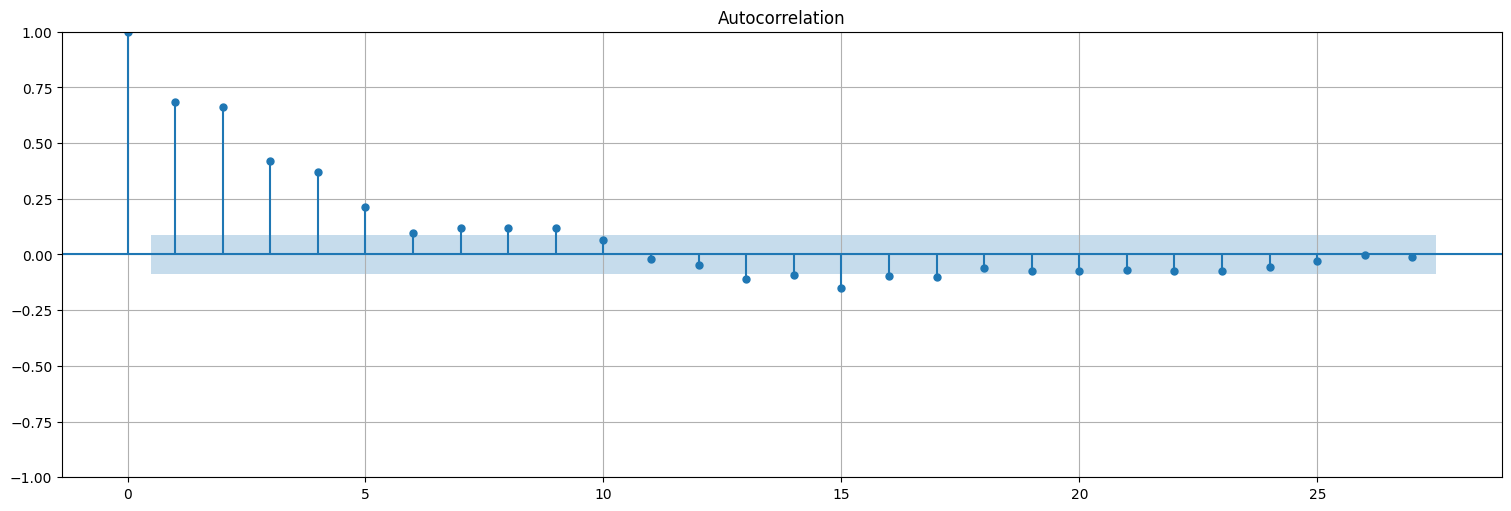
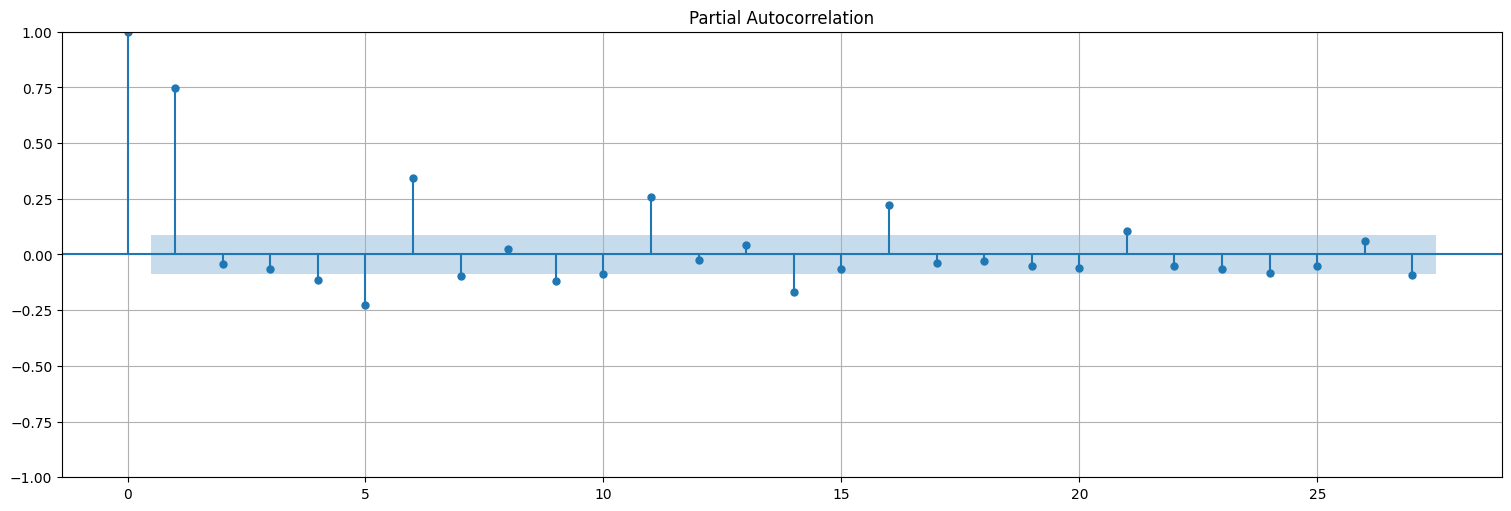
En cambio, la PACF no tiene el mismo comportamiento:

plot_pacf(x);

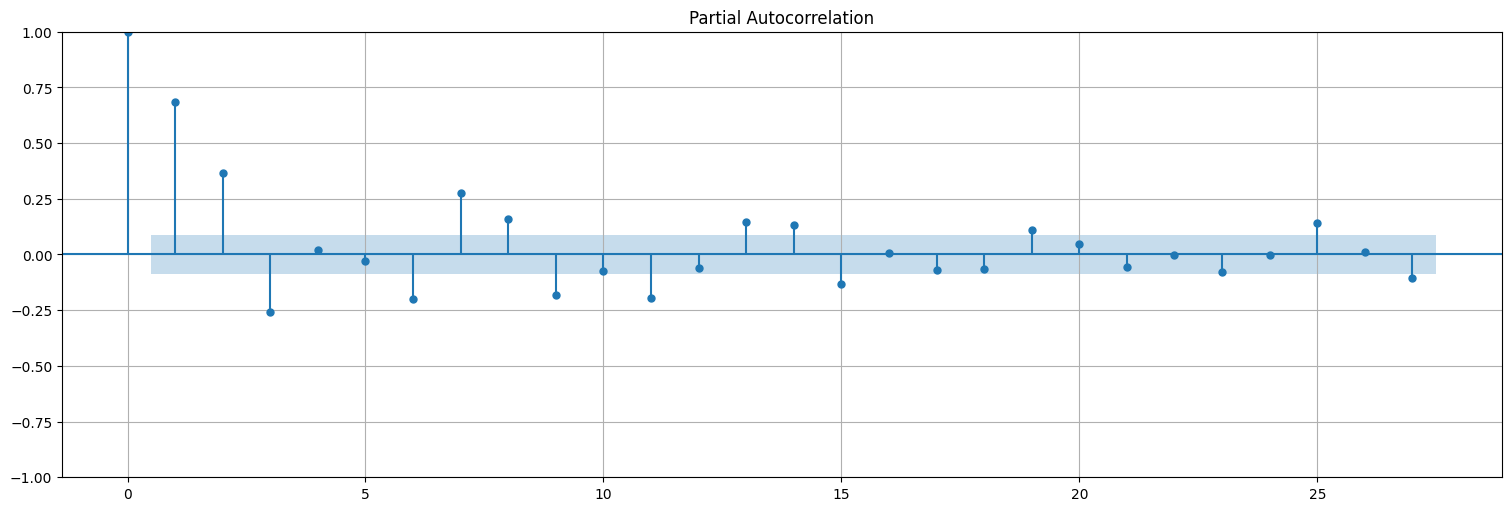
Otro ejemplo:

Consideremos la media móvil $\(x_t = \frac{1}{5}\left(w_t + w_{t-1} + w_{t-2} + w_{t-3} + w_{t-4}\right).\)$

n=5
x=arma_generate_sample([n],np.ones(n),500)
x=pd.Series(x)
plot_acf(x, bartlett_confint=False);

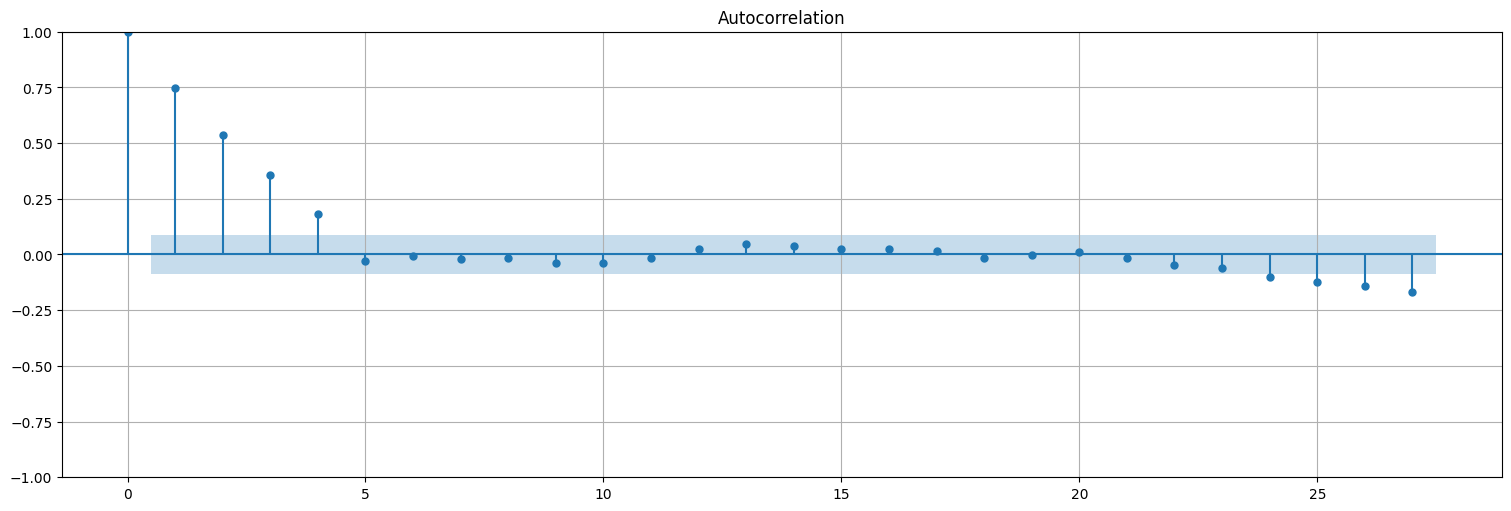
plot_pacf(x);

Resumen:

En el proceso \(MA(q)\) :

• La función de autocorrelación tiene \(q\) lags activos.

• La función de autocorrelación parcial decae lentamente

Es decir, a la inversa de lo que ocurre en AR.

Ajuste de un proceso \(MA(q)\)

Comencemos por el \(MA(1)\) dado por:

\[x_t = w_t + \theta w_{t-1}.\]

El proceso \(w_t\) no es directamente observable, entonces no podemos hacer una regresión a sus valores anteriores. Deberíamos “despejar” \(w_t\) de algún modo.

Observemos la siguiente recursión:

\[\begin{split} \left.\begin{array}{c} x_t = w_t + \theta w_{t-1} \\ x_{t-1} = w_{t-1} + \theta w_{t-2}\end{array}\right\} \Rightarrow x_t = w_t + \theta x_{t-1} -\theta^2 w_{t-2}\end{split}\]

Siguiendo la recursión, si \(|\theta|<1\) el modelo se dice invertible y podemos escribir:

\[ x_{t} = \sum_{j=1}^\infty (-\theta)^j x_{t-j} +w_t\]

es decir, convertimos un \(MA(1)\) en un \(AR(\infty)\) en cierto modo. Como \(\theta^j\) es decreciente, podríamos hacer una regresión y tratar de adivinar \(\theta\).

Problema: Es no lineal en \(\theta\) lo que estamos buscando.

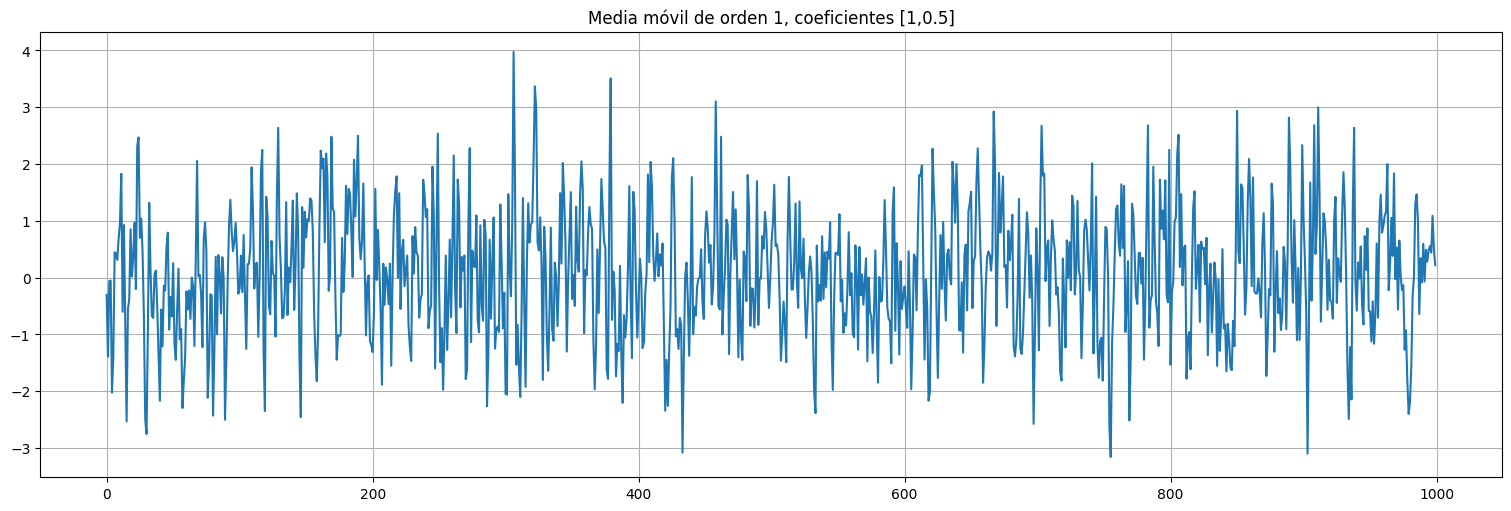
## Ejemplo: simulo un MA(1) con theta = 0.5 y hago varios fits
theta=0.5
x=arma_generate_sample([1],[1,theta],1000)
x=pd.Series(x)
x.plot(title=f"Media móvil de orden 1, coeficientes [1,{theta}]");

from statsmodels.formula.api import ols

data = pd.concat([x, x.shift(1)], axis=1).dropna()
data.columns = ["x", "xL1"]

fit = ols("x ~ 0+xL1", data=data).fit()
print(f"MSE de los residuos: {fit.mse_resid}")
fit.summary()

MSE de los residuos: 1.0609713538139918

OLS Regression Results

Dep. Variable:	x	R-squared (uncentered):	0.145
Model:	OLS	Adj. R-squared (uncentered):	0.144
Method:	Least Squares	F-statistic:	168.6
Date:	Mon, 19 May 2025	Prob (F-statistic):	9.87e-36
Time:	16:23:04	Log-Likelihood:	-1446.6
No. Observations:	999	AIC:	2895.
Df Residuals:	998	BIC:	2900.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
xL1	0.3801	0.029	12.984	0.000	0.323	0.438

Omnibus:	0.871	Durbin-Watson:	1.891
Prob(Omnibus):	0.647	Jarque-Bera (JB):	0.951
Skew:	0.060	Prob(JB):	0.622
Kurtosis:	2.909	Cond. No.	1.00

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

data = pd.concat([x, x.shift(1), x.shift(2)], axis=1).dropna()
data.columns = ["x", "xL1", "xL2"]

fit = ols("x ~ 0+xL1+xL2", data=data).fit()
print(f"MSE de los residuos: {fit.mse_resid}")
fit.summary()

MSE de los residuos: 1.0398252548742162

OLS Regression Results

Dep. Variable:	x	R-squared (uncentered):	0.162
Model:	OLS	Adj. R-squared (uncentered):	0.160
Method:	Least Squares	F-statistic:	96.22
Date:	Mon, 19 May 2025	Prob (F-statistic):	6.22e-39
Time:	16:23:04	Log-Likelihood:	-1434.6
No. Observations:	998	AIC:	2873.
Df Residuals:	996	BIC:	2883.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
xL1	0.4341	0.031	13.851	0.000	0.373	0.496
xL2	-0.1427	0.031	-4.553	0.000	-0.204	-0.081

Omnibus:	1.410	Durbin-Watson:	1.962
Prob(Omnibus):	0.494	Jarque-Bera (JB):	1.400
Skew:	0.030	Prob(JB):	0.497
Kurtosis:	2.826	Cond. No.	1.49

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

data = pd.concat([x, x.shift(1), x.shift(2), x.shift(3)], axis=1).dropna()
data.columns = ["x", "xL1", "xL2", "xL3"]

fit = ols("x ~ 0+xL1+xL2+xL3", data=data).fit()
print(f"MSE de los residuos: {fit.mse_resid}")
fit.summary()

MSE de los residuos: 1.0243813974085563

OLS Regression Results

Dep. Variable:	x	R-squared (uncentered):	0.176
Model:	OLS	Adj. R-squared (uncentered):	0.174
Method:	Least Squares	F-statistic:	70.79
Date:	Mon, 19 May 2025	Prob (F-statistic):	1.71e-41
Time:	16:23:04	Log-Likelihood:	-1425.2
No. Observations:	997	AIC:	2856.
Df Residuals:	994	BIC:	2871.
Df Model:	3
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
xL1	0.4531	0.031	14.406	0.000	0.391	0.515
xL2	-0.1987	0.034	-5.848	0.000	-0.265	-0.132
xL3	0.1288	0.031	4.095	0.000	0.067	0.190

Omnibus:	2.844	Durbin-Watson:	1.982
Prob(Omnibus):	0.241	Jarque-Bera (JB):	2.494
Skew:	0.030	Prob(JB):	0.287
Kurtosis:	2.762	Cond. No.	1.81

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Problema: el procedimiento anterior no es muy práctico, y si quisiéramos hacer regresión no lineal necesitamos un buen estimador inicial de \(\theta\). Además no generaliza bien a \(q\).

Método de los momentos: es otra idea válida, recordemos la función de autocorrelación del \(MA(1)\).

\[\begin{split}\rho(h) = \left\{\begin{array}{ll}1 & h=0\\ \frac{\theta}{1+\theta^2} & h=\pm 1 \\ 0 & \text{en otro caso}\end{array}\right.\end{split}\]

Si estimamos la correlación de orden uno de los datos (es decir la acf(x) en el lag \(1\)) podemos plantear:

\[\hat{\rho} (1) = \hat{\rho} = \frac{\theta}{1+\theta^2},\]

y despejar \(\theta\): $\(\hat{\rho} \theta^2 - \theta + \hat{\rho} = 0.\)$

Es decir: $\(\theta = \frac{1 \pm \sqrt{1-4\hat{\rho}^2}}{2 \hat{\rho}}.\)$

Observación: dos soluciones!! ¿Cuál elijo? ¿Y además qué pasa si da complejo?

• Se elije la “invertible”, es decir aquella que da menor a \(1\).

• En teoría \(\rho(1)<0.5\) si \(\theta<1\) entonces no puede dar complejo. Pero al estimar \(\rho\) por \(\hat{\rho}\) puede ocurrir.

• Para estimar \(\sigma^2_w\), la varianza del ruido, podemos usar que \(\sigma^2_x = (1+\theta^2)\sigma^2_w\) y usar el valor de \(\theta\) estimado.

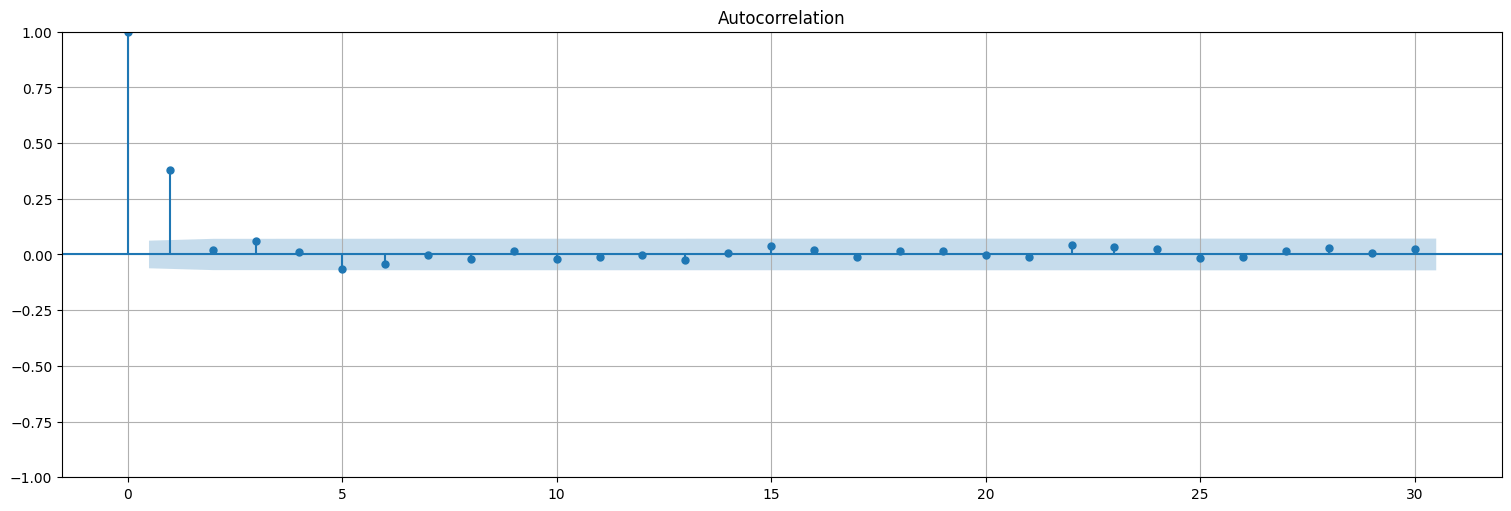
#### Ejemplo
from statsmodels.tsa.api import acf
plot_acf(x)
rho = acf(x)[1]
theta = (1-np.sqrt(1-4*rho**2))/(2*rho)

print(f"Autocorrelación estimada a lag 1: ρ(1)={rho}")
print(f"Ajuste por método de los momentos: θ={theta}")

Autocorrelación estimada a lag 1: ρ(1)=0.3776200114621945
Ajuste por método de los momentos: θ=0.4562147976238853

# Estimo la varianza del ruido por método de los momentos despejando (debería dar 1 en este caso).
sigma_w2 = np.var(x)/(1+theta**2)
print(f"Varianza estimada de wt: {sigma_w2}")

Varianza estimada de wt: 1.0204510256747432

• El método de los momentos se puede generalizar a mayor orden, y también se puede utilizar en el caso \(AR(p)\) (donde se denominan Ecuaciones de Yule-Walker).

• Sin embargo, en la práctica, estos estimadores no son los más eficientes. En general, si los ruidos son gaussianos, conviene usar un enfoque de máxima verosimilitud. Este es el método que utiliza la biblioteca statsmodels de python.

• Discutiremos más este método en relación al modelo completo ARMA, pero a modo de adelanto, hagamos el fit de este último modelo por máxima verosimilitud.

# Ejemplo
from statsmodels.tsa.api import ARIMA

#La funcion ARIMA permite ajustar modelos autorregresivos integrados y de media móvil. 
#En este caso solo usamos el coeficiente de media móvil.
#El parámetro trend="n" es porque el proceso ya está centrado (le sacamos el intercept)
fit = ARIMA(x,order=(0,0,1), trend="n").fit()
fit.summary()

SARIMAX Results

Dep. Variable:	y	No. Observations:	1000
Model:	ARIMA(0, 0, 1)	Log Likelihood	-1429.552
Date:	Mon, 19 May 2025	AIC	2863.104
Time:	16:23:04	BIC	2872.920
Sample:	0	HQIC	2866.835
	- 1000
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
ma.L1	0.4676	0.028	16.444	0.000	0.412	0.523
sigma2	1.0212	0.049	21.008	0.000	0.926	1.116

Ljung-Box (L1) (Q):	0.09	Jarque-Bera (JB):	2.33
Prob(Q):	0.77	Prob(JB):	0.31
Heteroskedasticity (H):	0.94	Skew:	0.04
Prob(H) (two-sided):	0.59	Kurtosis:	2.78

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

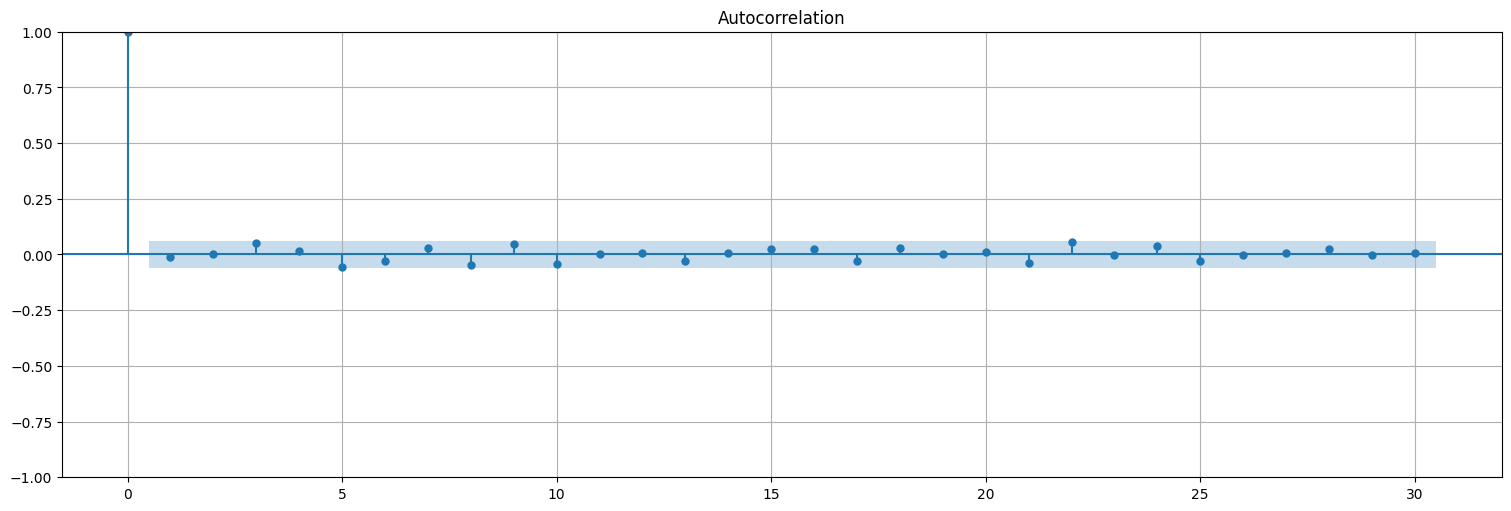
Podemos ver que la autocorrelación de los residuos se asemeja al ruido blanco:

res = fit.resid
plot_acf(res, bartlett_confint=False);

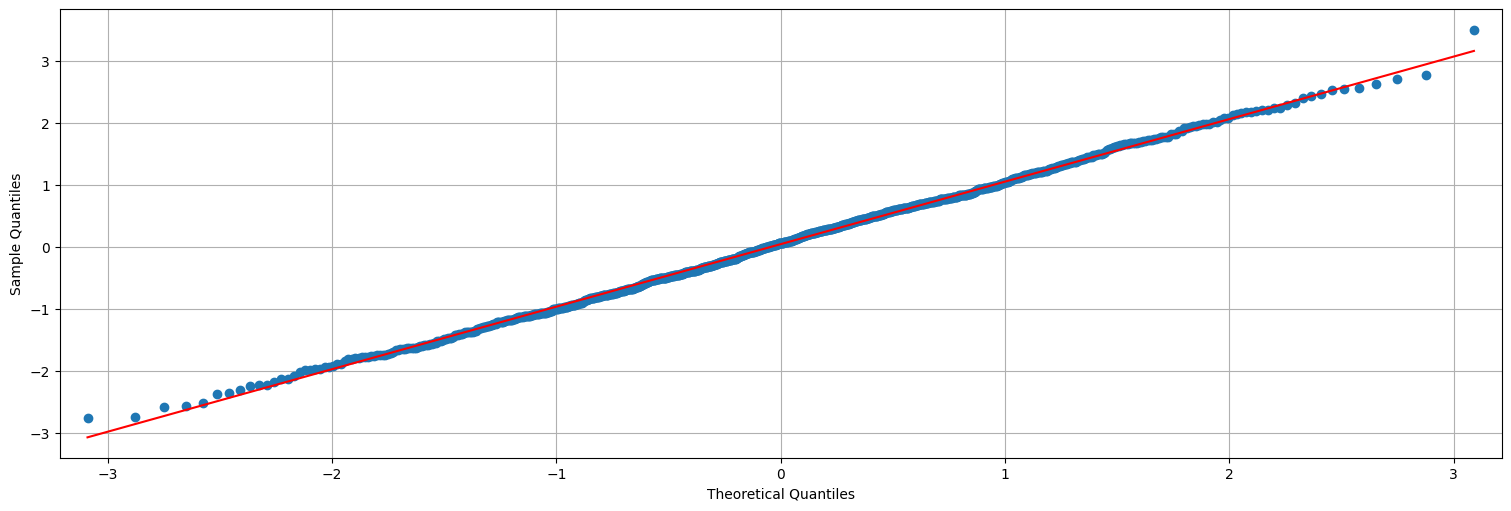
Y que los residuos son aproximadamente Gaussianos:

from statsmodels.graphics.api import qqplot
qqplot(res,line="s");

Modelos ARMA

Un modelo \(ARMA(p,q)\) es simplemente la combinación de los dos modelos vistos anteriormente. En términos matemáticos, \(x_t\) es un modelo ARMA si se verifica:

\[x_t = \phi_1 x_{t-1} + \ldots + \phi_p x_{t-p} + w_t + \theta_1 w_{t-1} + \ldots + \theta_q w_{t-q}\]

con \(\phi_p\) y \(\theta_q\) distintos de \(0\). Los coeficientes \(\phi_j\) son los coeficientes de la parte autorregresiva, y los \(\theta_j\) los de la parte media móvil. Como siempre, \(w_t\) es ruido blanco (gaussiano) de varianza \(\sigma^2_w\).

Notación alternativa

Recordemos que podemos reescribir la ecuación anterior como:

\[x_t - \phi_1 x_{t-1} - \ldots - \phi_p x_{t-p} = w_t + \theta_1 w_{t-1} + \ldots + \theta_q w_{t-q}\]

O bien:

\[\sum_{i=0}^p a_i x_t = \sum_{j=0}^q b_j w_j\]

Identificando \(a_0=1\), \(a_i = -\phi_i\), \(b_0=1\) y \(b_j = \theta_j\). Esta es la parametrización estándar en python.statsmodels.

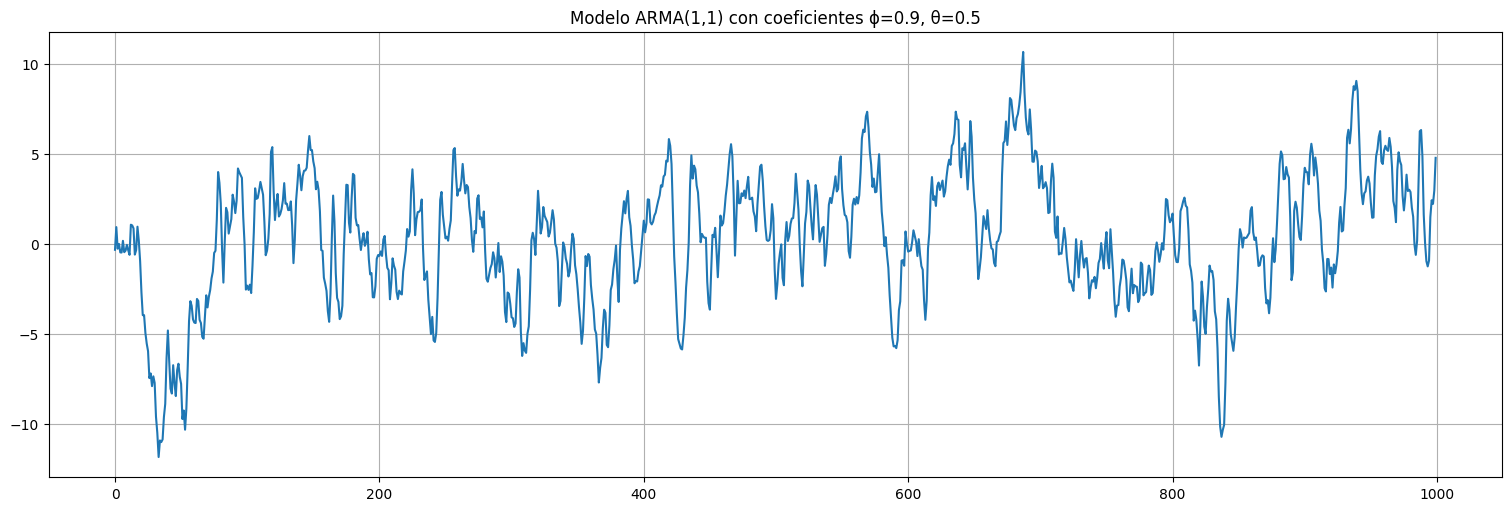
Ejemplo: ARMA(1,1)

Consideremos el siguiente proceso:

\[x_t = \phi x_{t-1} + w_t + \theta w_{t-1},\]

o bien

\[x_t - \phi x_{t-1} = w_t + \theta w_{t-1}\]

## Ejemplo: ARMA(1,1)
phi=0.9
theta=0.5
x=arma_generate_sample([1,-phi],[1,theta],1000)
x=pd.Series(x)
x.plot(title=f"Modelo ARMA(1,1) con coeficientes ϕ={phi}, θ={theta}");

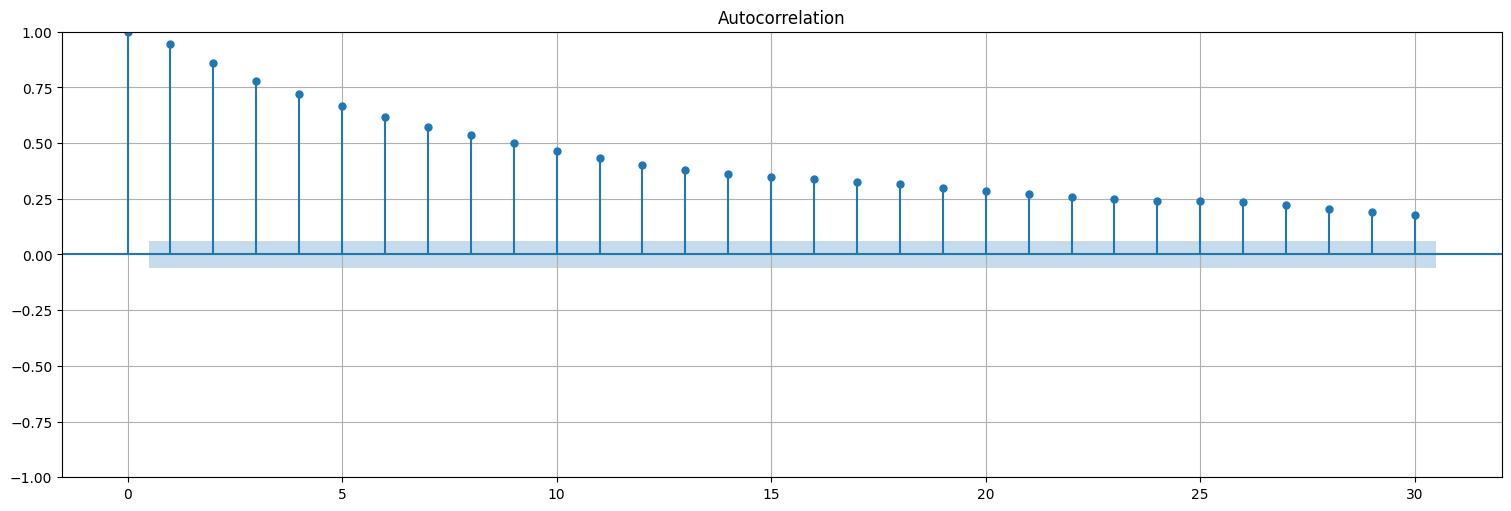
plot_acf(x,bartlett_confint=False);

plot_pacf(x);

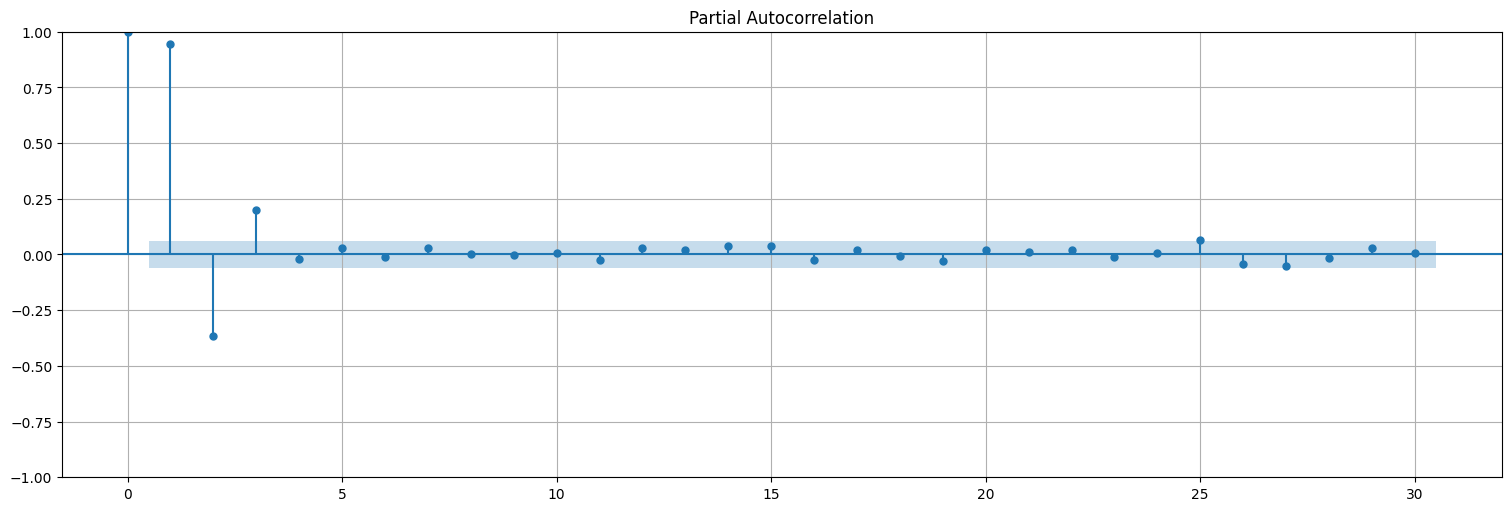
Problema: Ahora la ACF y PACF no son tan claros estimadores del orden del modelo!!

En general, para un modelo ARMA(p,q) tanto las ACF como la PACF decaen a 0 exponencialmente.

Aquí no queda otra que “probar” el orden y cortar en base a algún criterio tipo el AIC o BIC.

Ajuste de un modelo ARMA(1,1)

fit = ARIMA(x,order=(1,0,1), trend="n").fit()
fit.summary()

SARIMAX Results

Dep. Variable:	y	No. Observations:	1000
Model:	ARIMA(1, 0, 1)	Log Likelihood	-1437.233
Date:	Mon, 19 May 2025	AIC	2880.466
Time:	16:23:04	BIC	2895.189
Sample:	0	HQIC	2886.062
	- 1000
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
ar.L1	0.9077	0.013	67.711	0.000	0.881	0.934
ma.L1	0.4810	0.029	16.499	0.000	0.424	0.538
sigma2	1.0344	0.046	22.353	0.000	0.944	1.125

Ljung-Box (L1) (Q):	0.03	Jarque-Bera (JB):	0.58
Prob(Q):	0.87	Prob(JB):	0.75
Heteroskedasticity (H):	0.93	Skew:	0.06
Prob(H) (two-sided):	0.54	Kurtosis:	2.99

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

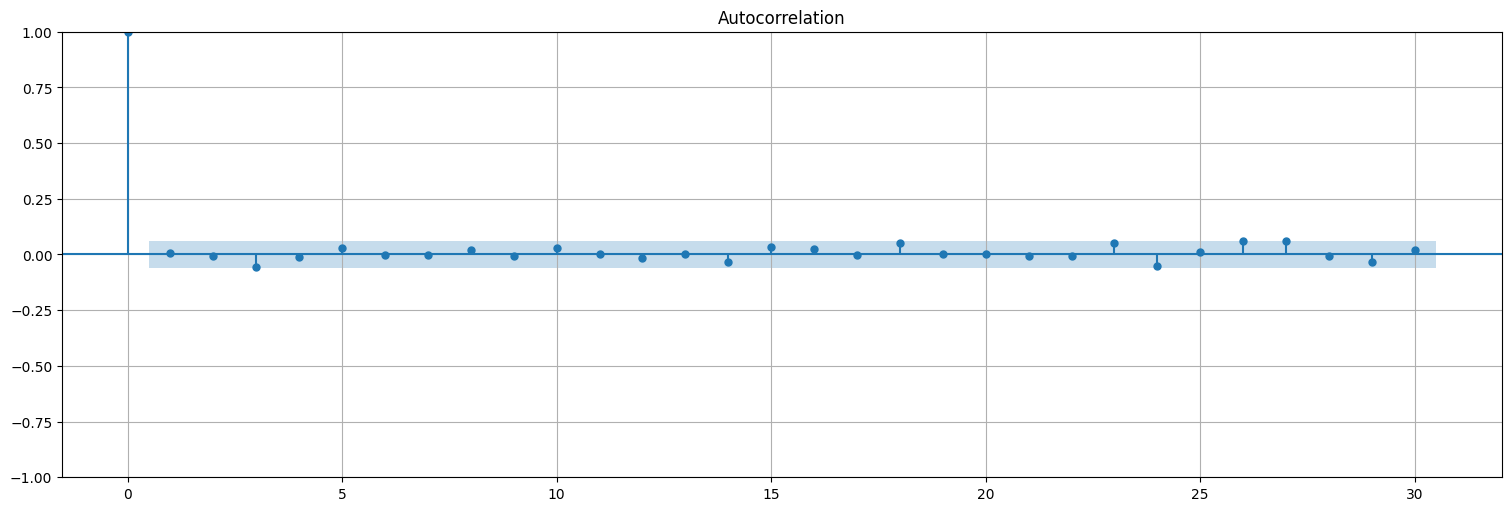
Podemos ver que la autocorrelación de los residuos se asemeja al ruido blanco:

res = fit.resid
plot_acf(res, bartlett_confint=False);

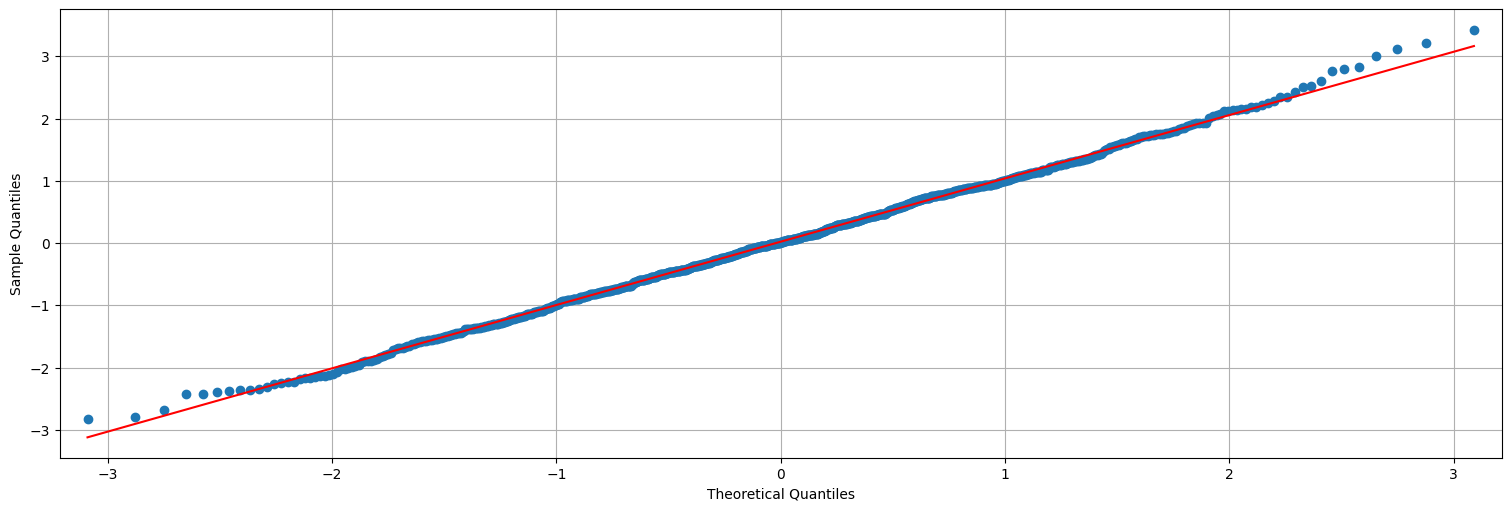
Y que los residuos son aproximadamente Gaussianos:

from statsmodels.graphics.api import qqplot
qqplot(res,line="s");

Causalidad, invertibilidad.

Observación: No todos los juegos de parámetros \(\phi_j\), \(\theta_j\) son posibles. Algunos juegos de parámetros pueden producir procesos no estacionarios, o con parámetros no bien definidos.

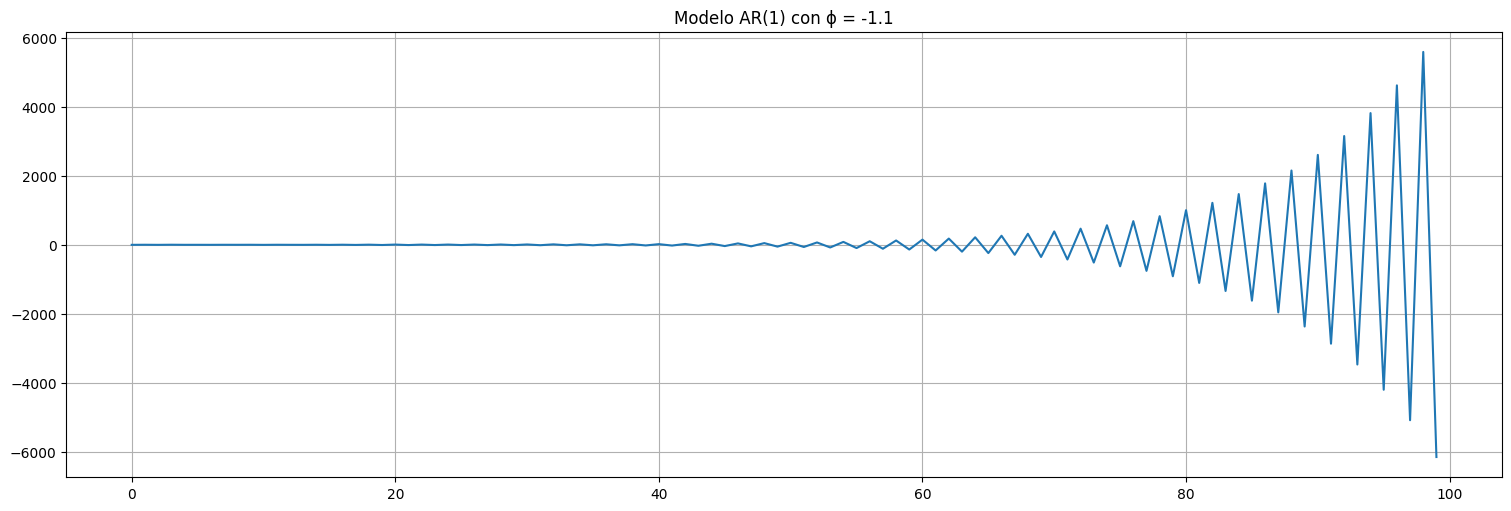
Ejemplo: Consideremos un proceso \(AR(1)\) con \(|\phi_1| > 1\), se tiene que:

\[x_t = \phi_1 x_{t-1} + w_t.\]

Este proceso amplifica el valor de la muestra anterior. Eventualmente explota!

# AR con explosion
phi=-1.1
x=arma_generate_sample([1,-phi],[1],100)
x=pd.Series(x)
x.plot()
plt.title(f"Modelo AR(1) con ϕ = {phi}");

Polinomios del AR y MA:

Se definen los siguiente polinomios, asociados a los coeficientes de la parte AR y MA:

\[\phi(z) = 1-\phi_1 z - \phi_2 z^2 -\ldots -\phi_p z^p,\]

\[\theta(z) = 1+\theta_1 z + \theta_2 z^2 + \ldots + \theta_q z^q.\]

Causalidad:

Un proceso ARMA es causal si se puede escribir solo como función de las innovaciones pasadas:

\[x_t = \sum_{j=0}^\infty \psi_j \phi_{t-j}.\]

con coeficientes \(\psi\) a determinar y \(\sum_{j=0}^\infty |\psi_j| <\infty\).

Teorema: Un proceso ARMA(p,q) es causal (no explosivo) si y solo si las raíces del polinomio \(\phi(z)\) están todas fuera del círculo unitario (es decir, |z|>1 en toda raíz).

Ejemplo: Si \(x_t\) es un AR(1), entonces \(\phi(z) = 1-\phi_1 z\), y la raíz está fuera de \([-1,1]\) si y solo si \(|\phi_1|<1\).

Invertibilidad:

Un proceso ARMA es invertible si se puede “despejar” \(w_t\) de los valores pasados del proceso:

\[w_t = \sum_{j=0}^\infty \pi_j x_{t-j},\]

con coeficientes \(\pi\) a determinar y \(\sum_{j=0}^\infty |\pi_j| <\infty\).

Teorema: Un proceso ARMA(p,q) es invertible si y solo si las raíces del polinomio \(\theta(z)\) están todas fuera del círculo unitario (es decir, |z|>1 en toda raíz).

## Ejemplos
from statsmodels.tsa.api import ArmaProcess

print("Ejemplo 1: AR(1) inestable")
proc = ArmaProcess.from_coeffs(-1.1,0)
print(proc)
print(f"Es estacionario? -> {proc.isstationary}")

print("Ejemplo 2: ARMA(1,1) como antes")
proc = ArmaProcess.from_coeffs(.9,.5)
print(proc)
print(f"Es estacionario? -> {proc.isstationary}")
print(f"Es invertible? -> {proc.isinvertible}")

Ejemplo 1: AR(1) inestable
ArmaProcess
AR: [1.0, 1.1]
MA: [1.0, 0.0]
Es estacionario? -> False
Ejemplo 2: ARMA(1,1) como antes
ArmaProcess
AR: [1.0, -0.9]
MA: [1.0, 0.5]
Es estacionario? -> True
Es invertible? -> True

Parámetros del ajuste de un modelo ARMA

El ajuste se realiza entonces mediante máxima verosimilitud o métodos de los momentos, buscando siempre un modelo causal e invertible.

Predicción en modelos ARMA

Idea: dado un modelo ARMA(p,q) de parámetros \(\phi_1,\ldots,\phi_p\) y \(\theta_1,\ldots,\theta_q\), y posiblemente una media \(\mu\), es decir un proceso:

\[ x_t - \mu = \phi_1 (x_{t-1} - \mu) + \ldots + \phi_p(x_{t-p}-\mu) + w_t + \theta_1 w_{t-1} + \ldots +\theta_q w_{t-q},\]

donde \(w_t\) es ruido blanco Gaussiano de varianza \(\sigma_w^2\).

Pregunta:

¿Cuál es la mejor predicción que uno puede hacer de \(x_{t+n}\) conociendo los valores del proceso \(x_0,\ldots,x_t\) y los parámetros?

El caso AR(p)

Supongamos \(\mu=0\) (en otro caso, simplemente centramos por la media). Este caso ya lo discutimos, si conocemos el proceso hasta tiempo \(n\), entonces sabemos que:

\[x_{n+1} = \phi_1 x_n +\ldots + \phi_p x_{n-p+1} + w_{n+1},\]

El mejor predictor \(\hat{x}_{n+1}^n\) en términos de error cuadrático medio es un predictor lineal:

\[\hat{x}_{n+1}^n = \alpha_0 + \sum_{k=1}^n \alpha_k x_k,\]

que debe satisfacer las ecuaciones de predicción:

\[E[(x_{n+1} - \hat{x}_{n+1}^n)x_k]=0 \quad \forall k=0,\ldots,n,\]

es decir, el error de predicción no debe estar correlacionado con ninguna de las muestras anteriores (extrajimos “toda la información”).

Notemos que es muy fácil resolver esto en el caso del \(AR(p)\) ya que tomando como predicción:

\[\hat{x}^n_{n+1} = \phi_1 x_n +\ldots + \phi_p x_{n-p+1},\]

se tiene que \(x_{n+1} - \hat{x}^n_{n+1} = w_{n+1}\) que sabemos no está correlacionado con ninguna muestra anterior!

Es decir, simplemente propagando la recursión como si el ruido fuera \(0\) obtenemos la mejor predicción (hay que demostrar esto para \(n+2\), \(n+3\), etc.)

El caso ARMA(p,q)

En el caso general no resulta tan sencillo resolver las ecuaciones de predicción, y debemos usar toda la historia del proceso. Consideremos el caso de predicción a un paso:

Construyo un estimador:

\[\hat{x}^n_{n+1} = \phi_{n1}x_n + \ldots +\phi_{nn}x_1 = \phi_n^T x\]

siendo \(x=(x_1,\ldots,x_n)\) el vector con todos los valores anteriores.

Planteando la ecuación de predicción queda:

\[E[(x_{n+1} - \sum_{j=1}^n \phi_{nj}x_{n+1-j})x_{n+1-k}] = 0, \quad k=1,\ldots,n.\]

Haciendo la distributiva queda:

\[E[x_{n+1}x_{n+1-k}] = \sum_{j=1}^n \phi_{nj}E[x_{n+1-j}x_{n+1-k}] = 0, \quad k=1,\ldots,n.\]

Identificando las covarianzas nos queda el siguiente sistema de ecuaciones:

\[\gamma(k) = \sum_{j=1}^n \phi_{nj}\gamma(k-j), \quad k=1,\ldots,n.\]

Lo anterior es un sistema de ecuaciones de la forma:

\[\Gamma_n \phi_n = \gamma_n.\]

Resolviendo el sistema salen los coeficientes.

Nota: debemos tener calculadas las covarianzas del modelo!

También se puede calcular la varianza del error de predicción para hacer intervalos de confianza, y queda:

\[P_{n+1}^n = \gamma(0) - \gamma_n^T \Gamma_n^{-1} \gamma_n.\]

Problema

La ecuación anterior solo explica como calcular “el paso siguiente” y aún así es muy difícil de resolver si el conjunto de datos es grande (sistema lineal grande). Afortunadamente ambos incovenientes se pueden levantar usando métodos recursivos:

• Algoritmo de Durbin-Levinson.

• Algoritmo de innovaciones.

Estos son los algoritmos que usan las bibliotecas de python para predecir. En particular, calculan:

• El mejor predictor lineal \(\hat{x}_{n+m}^n\) \(m\) muestras adelante.

• La varianza \(P^n_{n+m}\) del error, lo que permite construir intervaos de confianza.

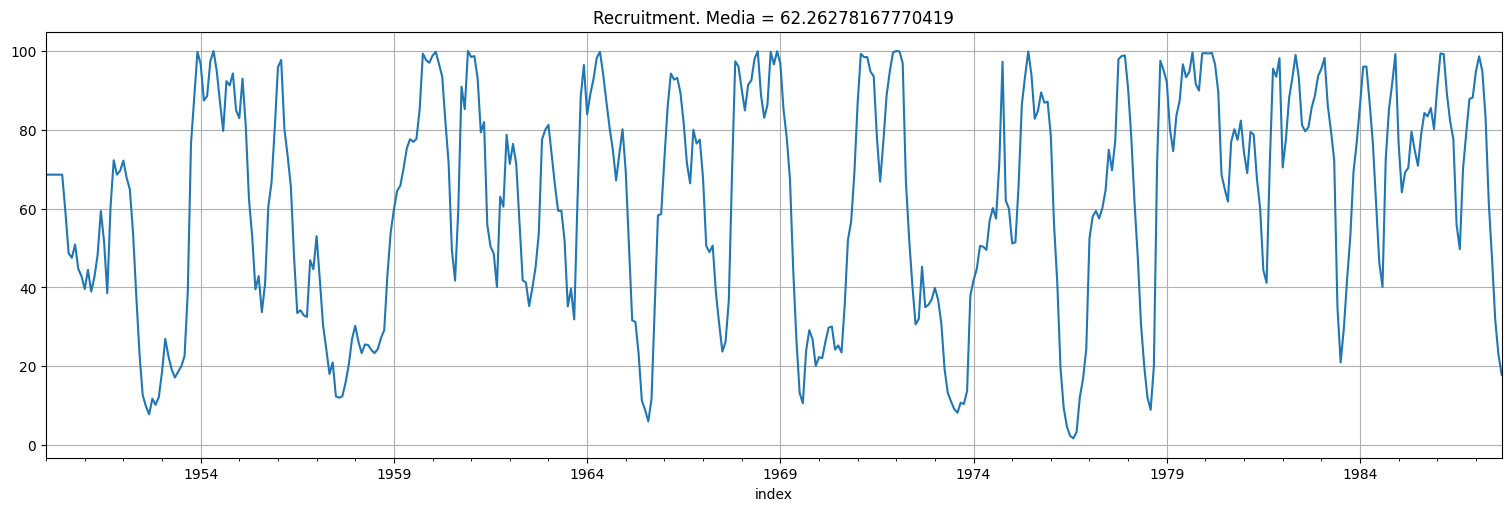
Ejemplo: la serie de Recruitment

rec=pd.Series(astsa.rec["value"])
rec.plot()
plt.title(f"Recruitment. Media = {np.mean(rec)}");

plot_pacf(rec);

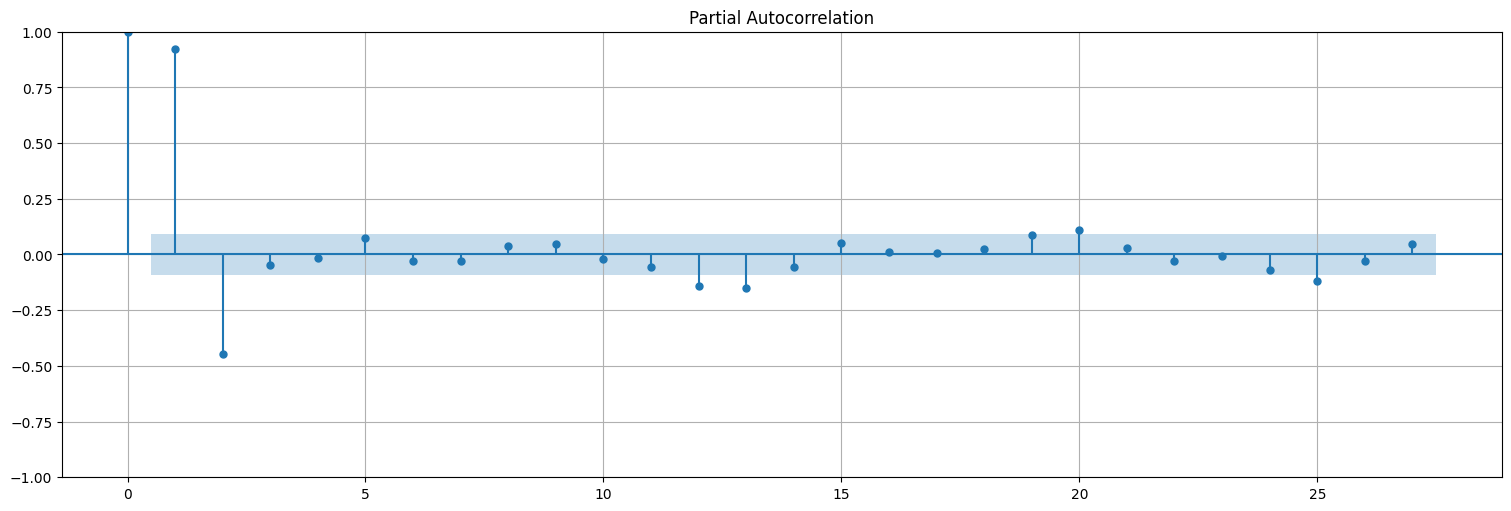
#Usamos la función de statsmodels para ajustar.
#trend="c" nos permite incorporar una tendencia constante (media) al fit.
from statsmodels.tsa.api import ARIMA
fit = ARIMA(rec,order=(2,0,0), trend="c").fit()
fit.summary()

SARIMAX Results

Dep. Variable:	value	No. Observations:	453
Model:	ARIMA(2, 0, 0)	Log Likelihood	-1661.510
Date:	Mon, 19 May 2025	AIC	3331.019
Time:	16:23:05	BIC	3347.483
Sample:	01-31-1950	HQIC	3337.506
	- 09-30-1987
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
const	61.8939	4.123	15.013	0.000	53.814	69.974
ar.L1	1.3512	0.041	32.952	0.000	1.271	1.432
ar.L2	-0.4612	0.037	-12.398	0.000	-0.534	-0.388
sigma2	89.3353	5.128	17.420	0.000	79.284	99.387

Ljung-Box (L1) (Q):	0.12	Jarque-Bera (JB):	93.63
Prob(Q):	0.72	Prob(JB):	0.00
Heteroskedasticity (H):	1.25	Skew:	0.30
Prob(H) (two-sided):	0.17	Kurtosis:	5.15

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

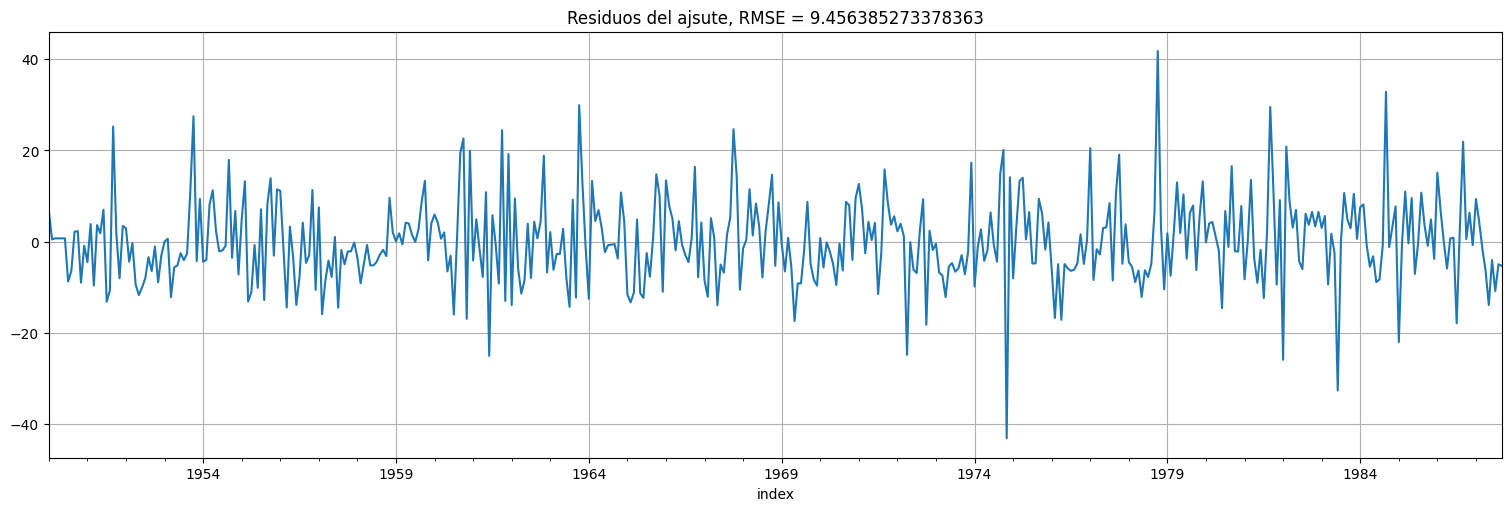
fit.resid.plot()
plt.title(f"Residuos del ajsute, RMSE = {np.sqrt(fit.mse)}");

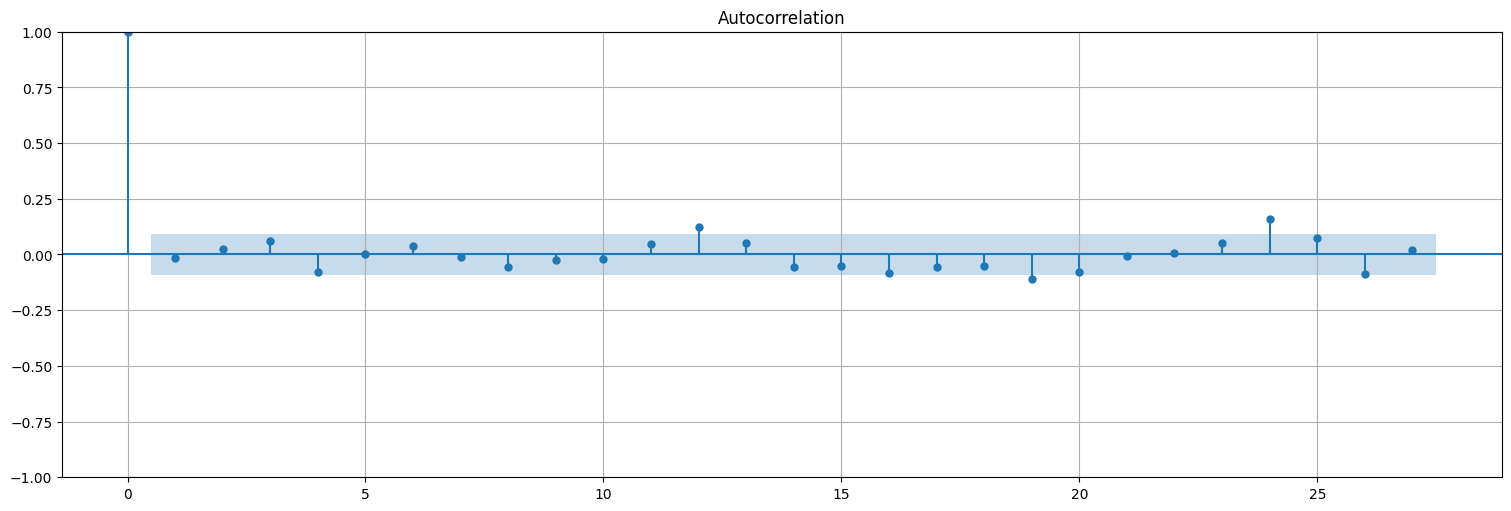
Podemos ver que la autocorrelación de los residuos se asemeja al ruido blanco:

res = fit.resid
plot_acf(res, bartlett_confint=False);

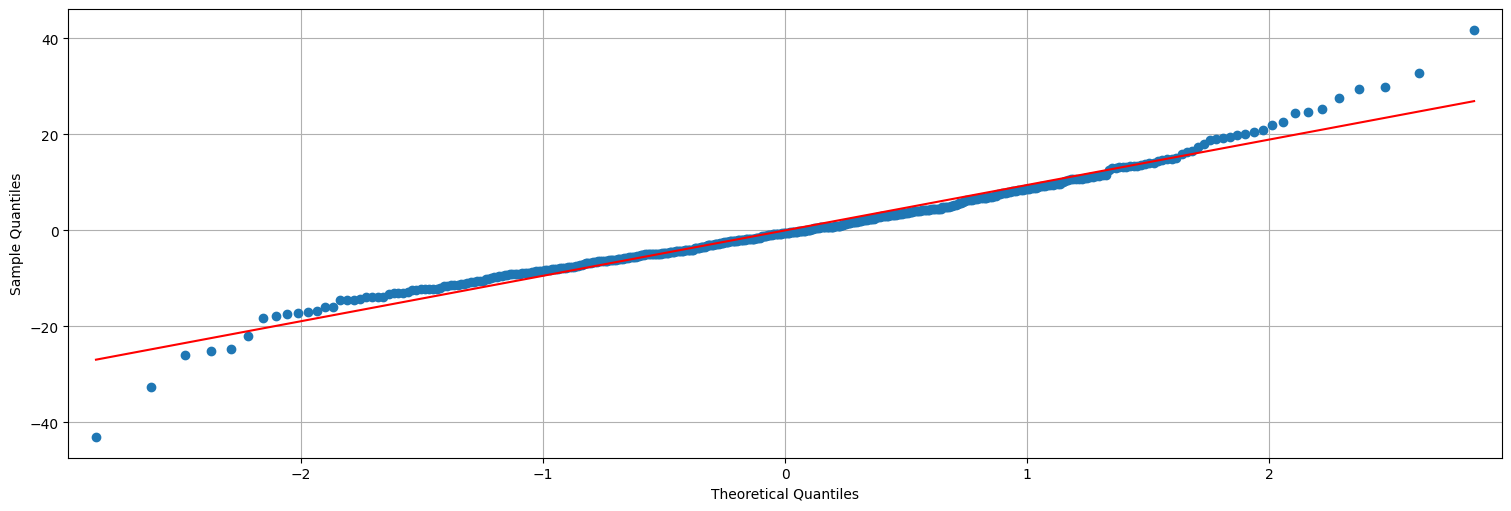
Y que los residuos son aproximadamente Gaussianos, pero ya no del todo. Tienen algunos outliers…

from statsmodels.graphics.api import qqplot
qqplot(res,line="s");

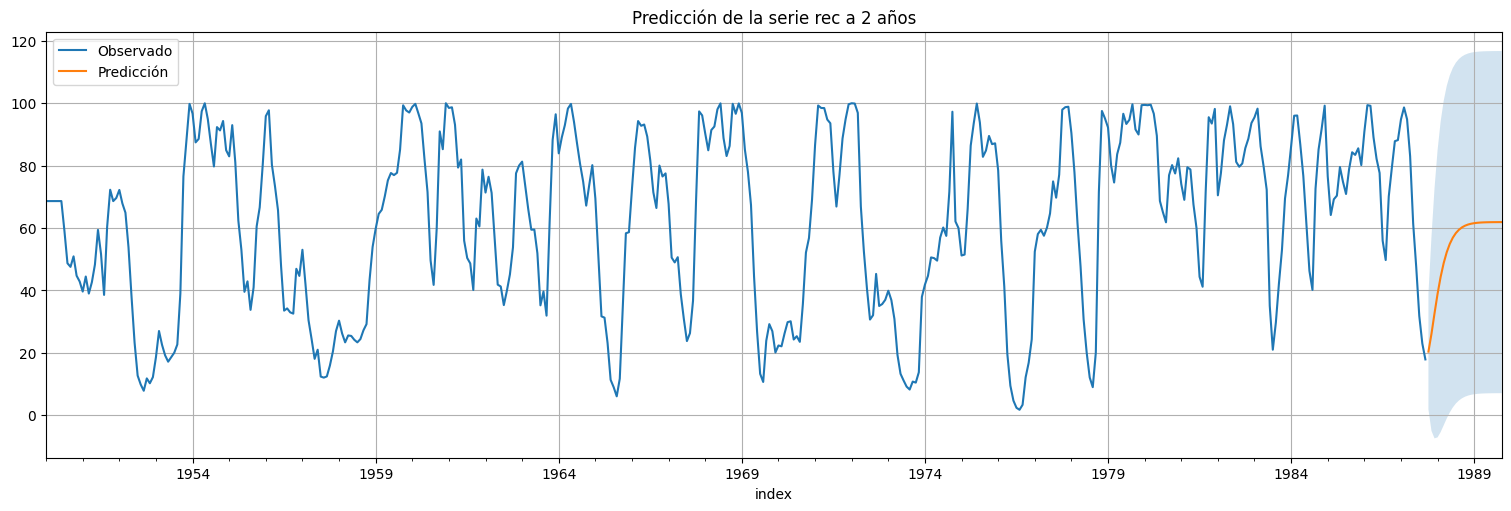
Predicción a futuro

Ahora que tenemos el modelo ajustado, ¿cómo podemos agregar nuevas predicciones usando los algoritmos mencionados?

#Usamos el modelo ajustado para predecir a futuro
h = 24 #horizonte de predicción
predicciones = fit.get_prediction(start=rec.size,end=rec.size+h)
xhat = predicciones.predicted_mean
confint = predicciones.conf_int(alpha=0.05) #alpha es la confianza del intervalo
rec.plot()
xhat.plot()
plt.legend(["Observado","Predicción"])
plt.fill_between(xhat.index,confint["lower value"], confint["upper value"], alpha=0.2);
plt.title("Predicción de la serie rec a 2 años");

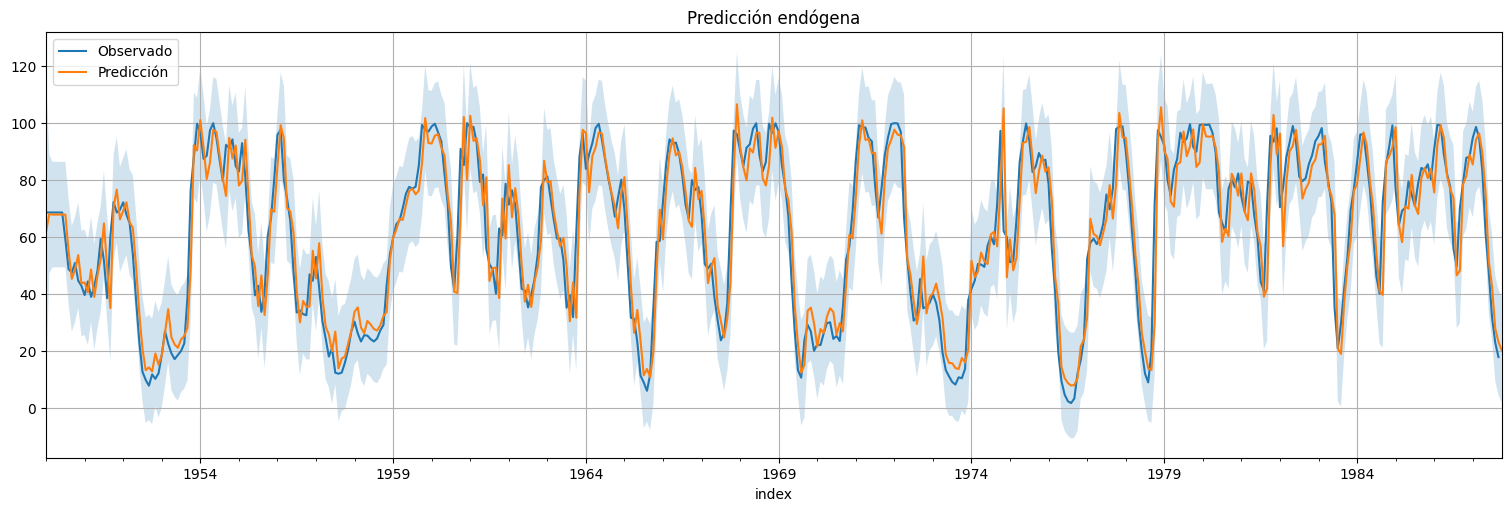
Predicción endógena de la serie

#Usamos el modelo ajustado para predecir los propios valores de la serie.
predicciones = fit.get_prediction(start=0,end=rec.size)
xhat = predicciones.predicted_mean
confint = predicciones.conf_int(alpha=0.05) #alpha es la confianza del intervalo
rec.plot()
xhat.plot()
plt.legend(["Observado","Predicción"])
plt.fill_between(xhat.index,confint["lower value"], confint["upper value"], alpha=0.2);
plt.title("Predicción endógena");

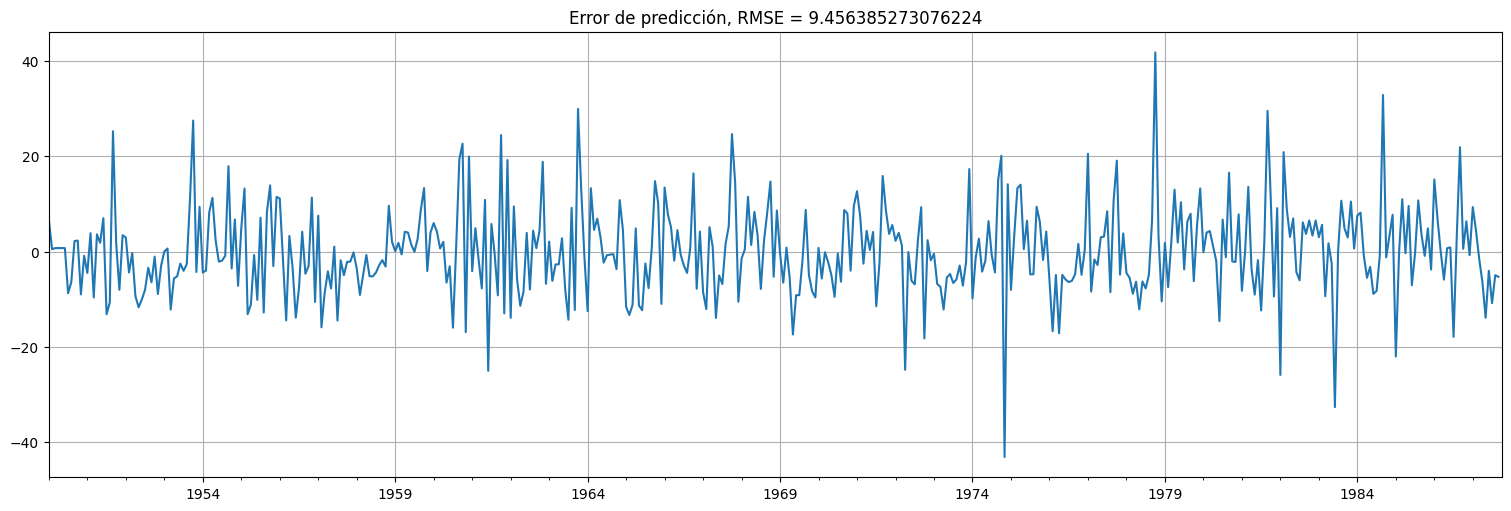
Podemos también ver el error de predicción, pero de hecho estos son exactamente los residuos del fit!

error = rec-xhat
error.plot()
plt.title(f"Error de predicción, RMSE = {np.std(error)}");

Ejercicios

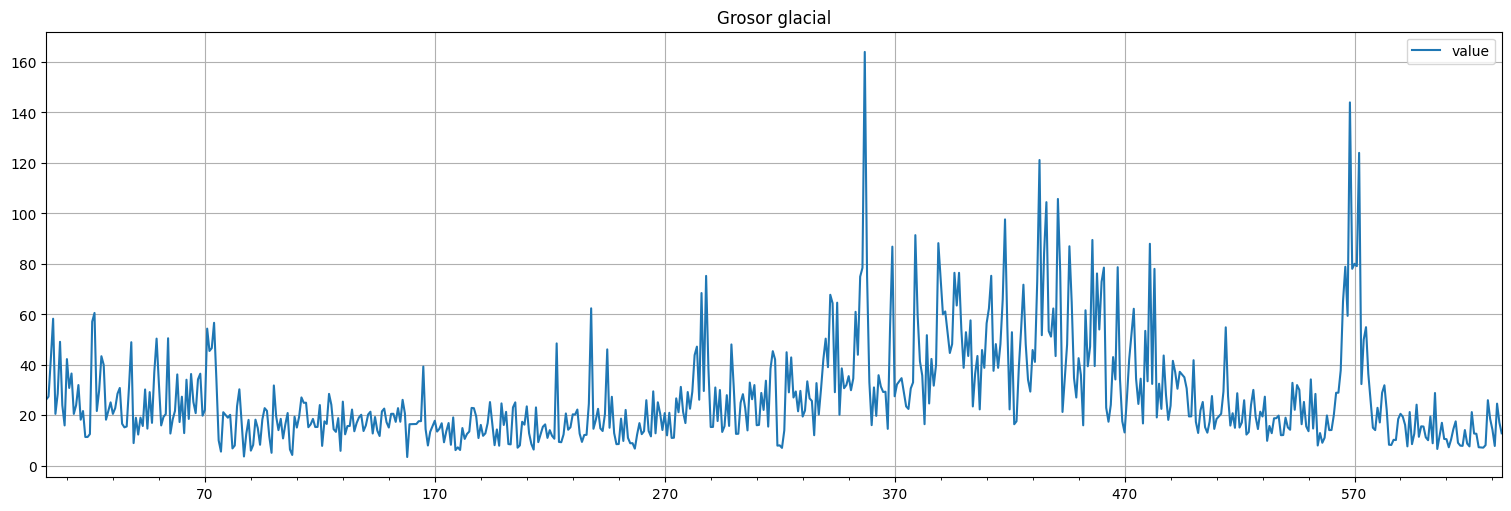
Análisis del grosor glacial.

Analizar la serie de grosor glacial del paquete astsa (serie varve). Aplicar la transformación diff(log(x)) para obtener una serie estacionaria y discutir el ajuste de un modelo \(MA(q)\) y \(ARMA(p,q)\).

varve=astsa.varve
varve.plot();
plt.title("Grosor glacial");