Introducción¶
Curso: Análisis Predictivo de Series Temporales
Posgrado de Big Data e Inteligencia Artificial
Universidad ORT Uruguay
Docente: Andrés Ferragut
Materiales¶
Libros del curso:
Materiales de referencia:
Sitio de Github del curso. Siempre actualizado a los últimos materiales.
Equipo de Teams. Para discusiones, consultas, etc.
Sitio de Aulas de la asignatura.
Software¶
Para el desarrollo del curso: Jupyter notebooks + Python (antes R).
Material de ejemplo (acompañante del libro): https://www.stat.pitt.edu/stoffer/tsa4/
Evaluación¶
Ejercicios en clase (30 pts): Corresponden a una selección de los ejercicios al final de cada uno de los cuadernos de clase.
Obligatorio (40 pts): En grupo. Análisis de una serie de datos usando herramientas del curso o estudio de algún modelo/algoritmo que vaya un poco más allá de lo visto en clase.
Parcial (30 pts): Evaluación individual al final del curso.
Aprobación: Suma \(\geq\) 70.
Temario¶
Introducción
Regresión y análisis exploratorio de series.
Análisis espectral.
Modelos autorregresivos y de media móvil (ARMA)
Modelos ARIMA (ARMA integrado) para series no estacionarias.
Modelos en espacio de estados.
Machine learning aplicado a series.
Bibliotecas¶
astsa: Es la biblioteca de R que acompaña al libro, y tiene ejemplos de series de datos y herramientas para graficarlas, así como algunas de las herramientas de modelado.astsadata: Biblioteca de Python que incluye los datos deastsapara trabajar en Python.Instalación:
pip install astsadata
statsmodels: Biblioteca de análisis estadístico en Python.matplotlib,pandas,numpy,scipy: bibliotecas estándar de manejo de datos y gráficas en Python.
## Ejemplo: instalación de astsadata usando pip:
#!pip install astsadata
#Importo astsadata
import warnings
with warnings.catch_warnings(action="ignore"):
import astsadata as astsa
## Para las figuras
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [15,5]
plt.rcParams['axes.grid'] = True
Ejemplos de series temporales¶
A continuación presentamos varios ejemplos de series temporales a partir de datos reales para ilustrar las preguntas que buscamos contestar con las herramientas del curso.
Ejemplo 1: Ganancias trimestrales por acción de Johnson & Johnson.¶
21 años de datos (84 trimestres) desde 1960 a 1980.
jj = astsa.jj
jj.plot(xlabel="Año", ylabel="Valor", legend=False);
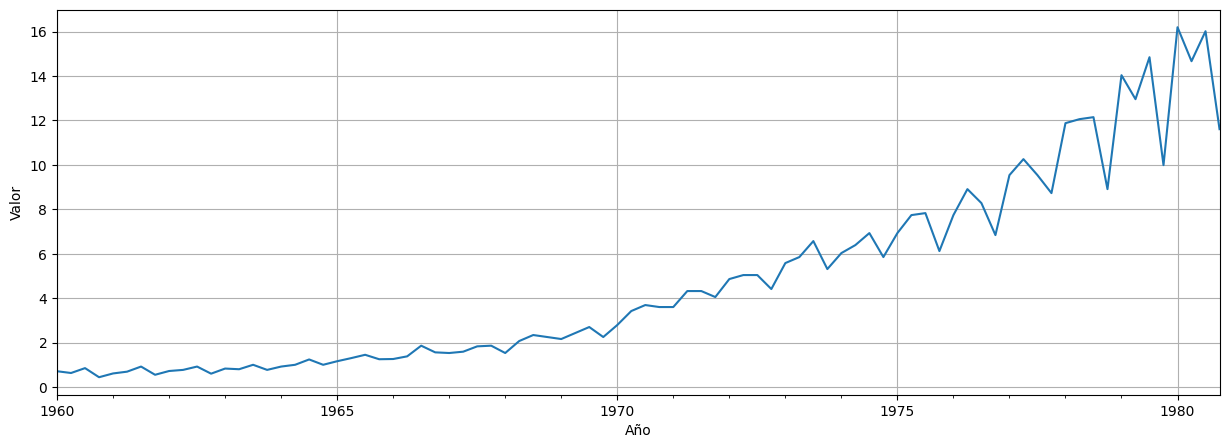
Observaciones¶
Hay una tendencia creciente a lo largo de la serie…¿cómo la detectamos?
Hay un comportamiento regular alrededor de dicha tendencia: cada 4 trimestres hay uno más bajo. ¿Cómo lo estimamos?
¿Podemos predecir el cuánto serán las ganancias en el futuro?
Ejemplo 2: Calentamiento global¶
Serie de datos de temperaturas medias anuales de 1880 a 2009, en relación al promedio 1951-1980, en grados centigrados.
globtemp = astsa.globtemp
globtemp.plot(xlabel="Año", ylabel="Global Temperature Deviations", legend=False, grid=True);
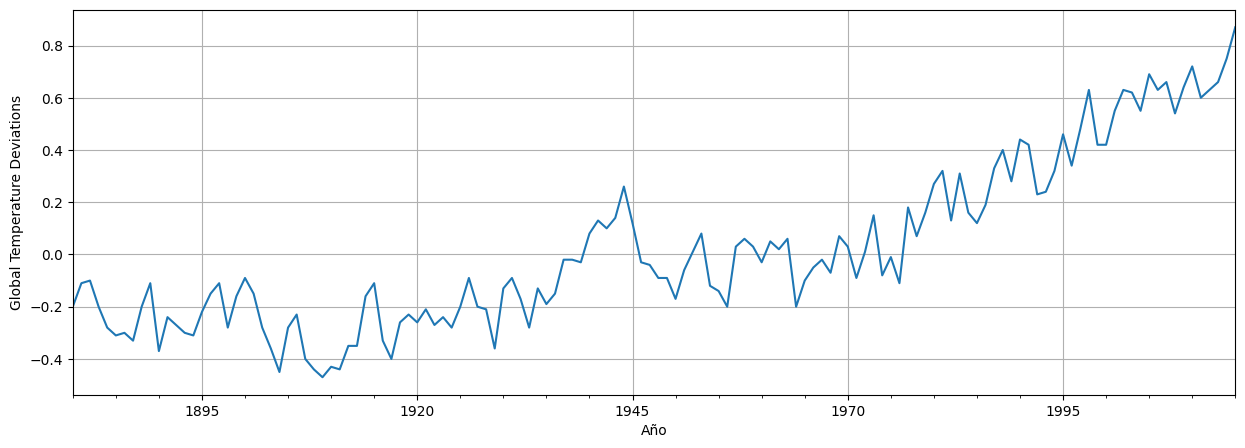
Observaciones¶
Parece haber una tendencia creciente, comenzando alrededor de 1970.
¿Esto confirma el calentamiento global?
¿Qué pasa si miramos escalas más largas de tiempo?
¿Es estadísticamente significativo el cambio?
Ejemplo 3: Precio de exportación del salmon¶
Serie de datos mensual con el precio de exportación del Salmón Noruego, en dólares por kilogramo, de Setiembre 2003 a Junio 2017
salmon = astsa.salmon
salmon.plot(xlabel="Año", ylabel="Valor", legend=False, grid=True);
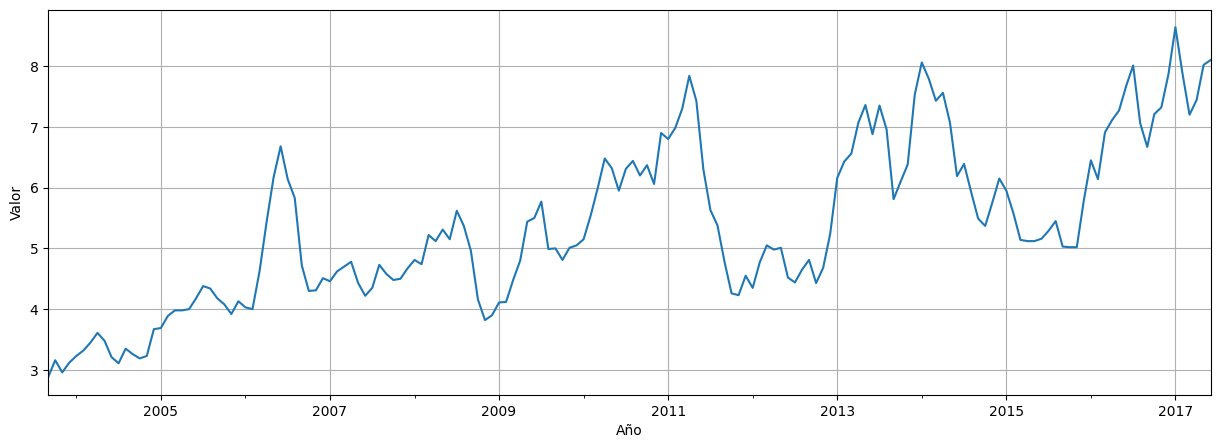
Observaciones:¶
Combina tendencia con ciclos de escala más lenta.
¿Cómo identificamos estos ciclos?
¿Cómo analizamos la dependencia de corto plazo?
Ejemplo 4: Señal acústica¶
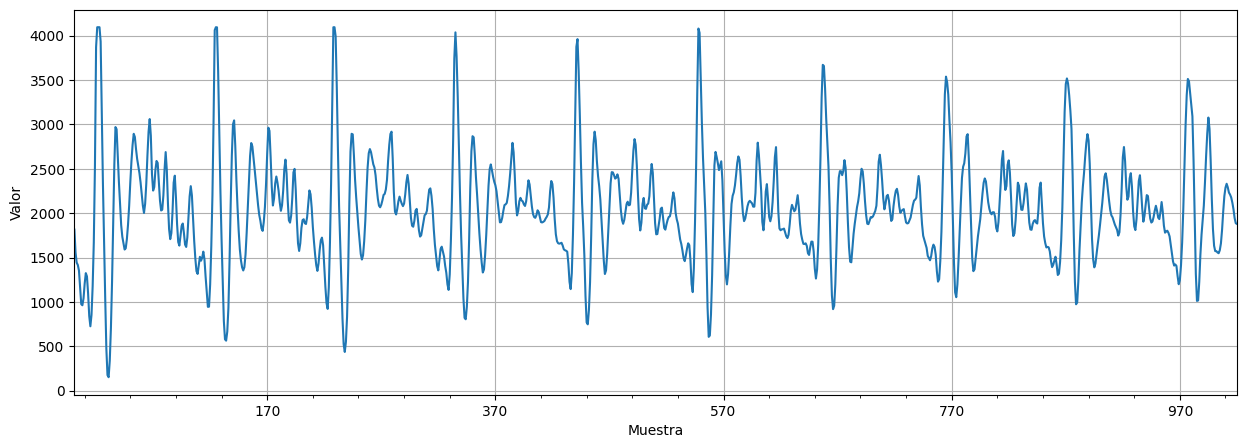
Señal de 1000 muestras (\(0.1s\)) de audio de la palabra “aaahhh”.
speech = astsa.speech
speech.plot(xlabel="Muestra", ylabel="Valor", legend=False, grid=True);
##Para reproducir el sonido:
from IPython.display import Audio
Audio(speech.value, rate=10000)
Observaciones¶
Señal con periodicidades importantes, debido al funcionamiento físico del sistema (sonido)
Estacionaria en el tiempo (mantiene las características)
El problema de interés puede ser reconocer las frecuencias involucradas.
También el fonema o estructura de lo que se habla.
Ejemplo 5: Dow Jones¶
Serie de retornos diarios (o cambio porcentual) del índice Dow Jones de 2006 a 2016.
import numpy as np
djiar = np.log(astsa.djia["Close"]).diff()
djiar.plot(title="Dow Jones Industrial Average Returns");
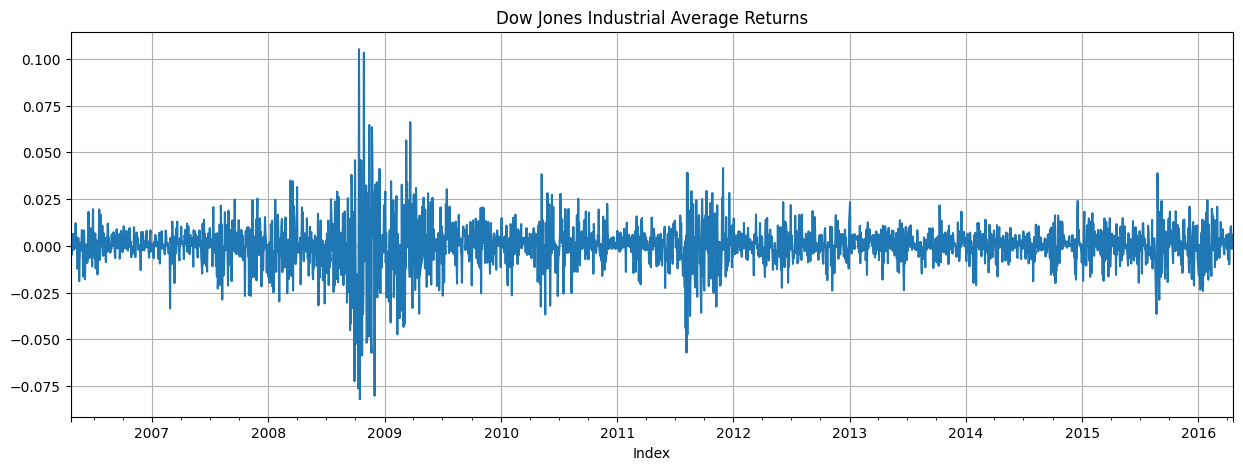
Observaciones:¶
Media de retornos estable, alrededor de 0 (es decir poca variación diaria).
Pero aparecen períodos de alta volatilidad (varianza).
Es de interés predecir este tipo de fenómenos.
A modo de ejemplo el pico alto corresponde a la crisis financiera de 2008.
Ejemplo 6: El niño y los peces¶
Este es un ejemplo de correlación entre fenómenos. Se tiene la serie de 1950-1987 del Southern Oscillation Index (vinculado a la temperatura del Océano Pacífico) así como a la población de peces (Recruitment)
soi = astsa.soi
rec = astsa.rec
fig, axs = plt.subplots(2, 1, constrained_layout = True)
soi.plot(ax=axs[0], xlabel="Year", title="Southern Oscillation Index")
rec.plot(ax=axs[1], xlabel="Year", title="Recruitement index", color="teal");
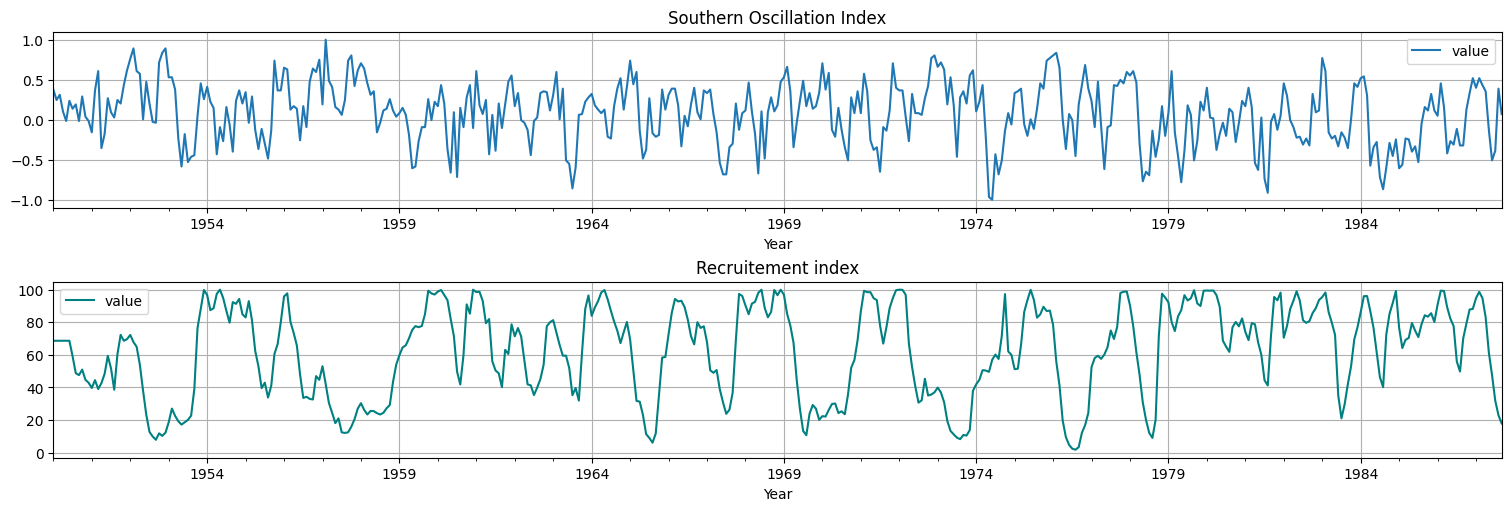
Observaciones¶
Comportamiento periódico, con ciclos regulares.
Varios períodos o frecuencias aparecen (por ej. en la 2a. parece haber dos frecuencias de oscilación, una rápida y una lenta.
Parece haber una correlación entre ambas series (valores altos de SOI llevan a valores bajos de peces).
¿Podemos usar una serie para predecir la otra?
Ejemplo 7: Terremotos y explosiones¶
Se tienen la serie de datos sismográficos de las ondas \(P\) (\(t=0\ldots 1000\)) y \(S\) (\(t=1000 \ldots 2000\)) correspondientes a un terremoto y una explosión.
EQ5 = astsa.EQ5
EXP6 = astsa.EXP6
fig, axs = plt.subplots(2, 1, constrained_layout = True)
EQ5.plot(ax=axs[0], xlabel="Time", title="Earthquake", legend=False)
EXP6.plot(ax=axs[1], xlabel="Time", title="Explosion", color="teal", legend=False);
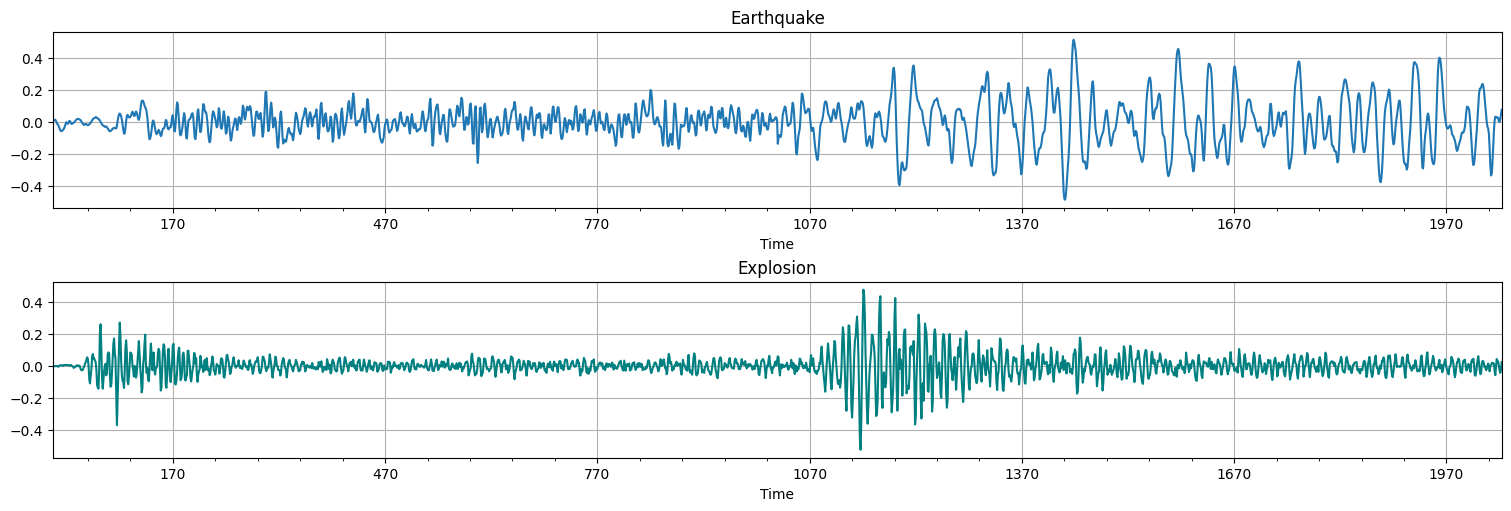
Observaciones:¶
Claramente las gráficas son distintas “a ojo”.
¿Podemos entrenar un algoritmo que distinga ambos fenómenos?
¿Podemos hacer que lo distinga en tiempo real?
¿Podemos clasificar automáticamente las series? ¿Cuáles son las características esenciales?
Ejemplo 8: Covid-19¶
import pandas as pd
data = pd.read_csv("https://raw.githubusercontent.com/GUIAD-COVID/datos-y-visualizaciones-GUIAD/master/datos/estadisticasUY.csv", index_col=[0], parse_dates=[0], date_format="%d/%m/%Y")
data["cantCasosNuevosAjustado"].plot(xlabel="Fecha", title="Casos nuevos reportados diarios de COVID-19 en Uruguay");
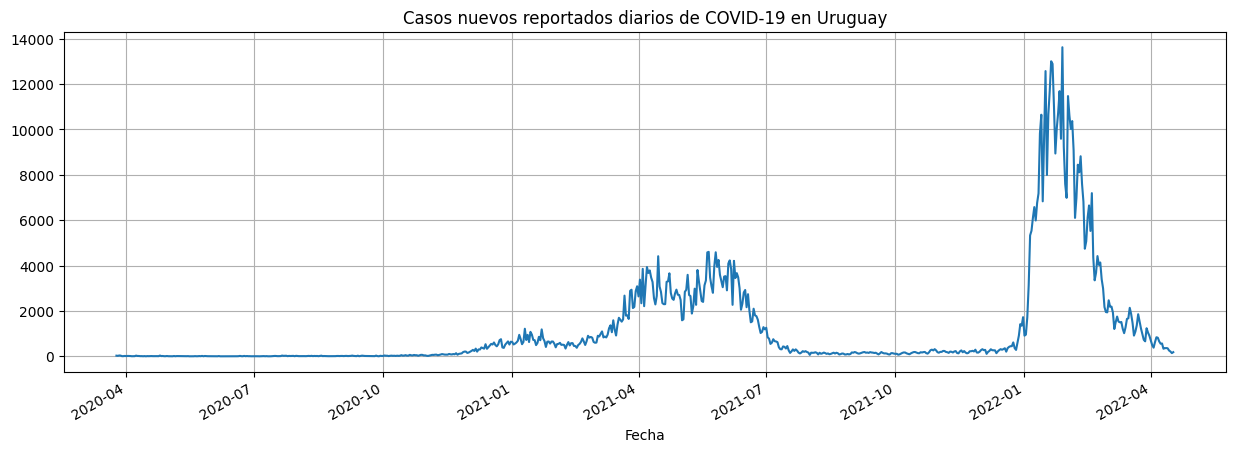
Observaciones:¶
Serie con fases bien diferenciadas:
Momentos de “relativo control”.
Momentos de crecimiento exponencial (olas) y luego descenso
Presenta picos producto de fenómenos intra-semana.
Una pregunta posible es: ¿Cómo detectamos el crecimiento exponencial?
¿Podemos explicar el comportamiento de la serie a partir de otros datos poblacionales? (Ej: movilidad)
Objetivos del curso¶
Proveer modelos matemáticos para el análisis de series temporales.
Fuerte base matemática para modelar los fenómenos más comunes.
Proveer herramientas para responder las preguntas anteriores.
Aprender los modelos clásicos de series. Ajuste, predicción de valores futuros, filtrado y suavizado, etc. etc.
Explorar técnicas más avanzadas (en particular en el trabajo obligatorio).