Modelos autorregresivos y autocorrelación parcial¶
Introducción:¶
En las clases anteriores introdujimos los conceptos de autocorrelación y correlación cruzada para analizar la relación entre una serie o series y sus versiones “laggeadas”.
Exploramos además cómo realizar regresiones lineales (con o sin lags) para explicar el comportamiento de una serie. Sirve para explicar tendencias, estacionalidad.
Generalmente esto es insuficiente para explicar el comportamiento de una serie con dinámica interna.
En general esto lo vimos como que “quedaba correlación” luego de los ajustes.
Objetivos:¶
Introducir la correlación como parte intrínseca de la serie. Hacer que los valores anteriores del proceso influyan directamente en el valor observado actual (autorregresivo, AR), y que valores anteriores del ruido influyan en el valor actual observado (media móvil, MA).
Combinaciones de los dos anteriores da lugar a los modelos ARMA.
Veremos cómo es posible:
Usar modelos ARMA para predecir valores futuros de una serie.
Ajustar los parámetros de un modelo ARMA a partir de observaciones.
Si agregamos el caso no estacionario, veremos como diferenciar una serie puede producir estacionariedad. Esto da lugar a los modelos ARIMA (I=integrated).
Definición:¶
Una serie temporal es una sucesión de variables aleatorias o proceso estocástico \(x_0,x_1,x_2,\ldots\). La variable aleatoria \(x_t\) denota el valor del proceso al tiempo \(t\).
Al proceso estocástico o serie temporal se lo denota por \(\{x_t\}\).
Típicamente (y para todo este curso) se consideran indexados por \(t\) entero (\(\ldots, -2, -1, 0, 1, 2, \ldots\)).
A los valores particulares que toma una serie temporal cuando la observamos se le denomina realización del proceso, y lo denotaremos por \(x_t\), abusando un poco de la notación.
Ruido blanco¶
Definición: El caso más sencillo de serie temporal es un conjunto de variables aleatorias con la misma distribución y no correlacionadas. Si \({w_t}\) es una serie temporal en la cual las variables tienen media \(E[w_t]=0\), varianza \(Var(w_t) = \sigma_w^2 >0\) y la covarianza de \(w_t\) y \(w_s\) es \(0\) se le denomina ruido blanco.
Definición: Si además las variables son independientes y con la misma distribución (iid), se le denomina ruido blanco independiente.
Definición: En el caso que además la distribución de \(w_t\) para cada \(t\) sea Normal \(N(0,\sigma_w^2)\) le llamamos ruido blanco gaussiano.
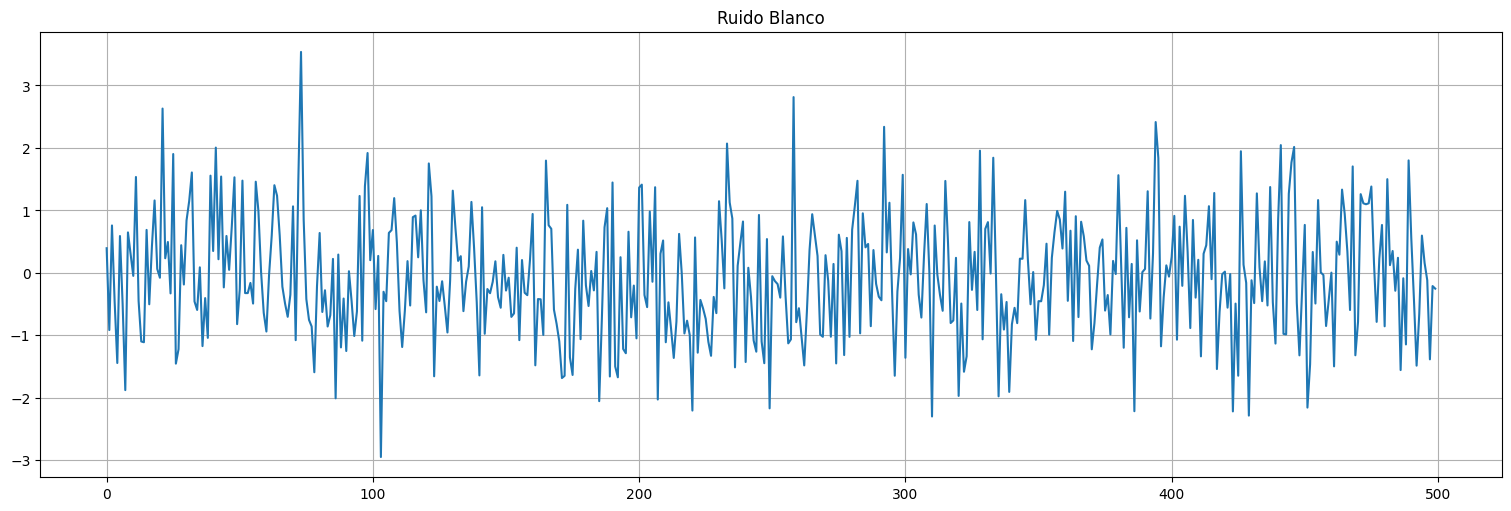
w = np.random.normal(loc=0,scale=1,size=500) #genero 500 muestras gaussianas
plt.plot(w)
plt.title("Ruido Blanco");
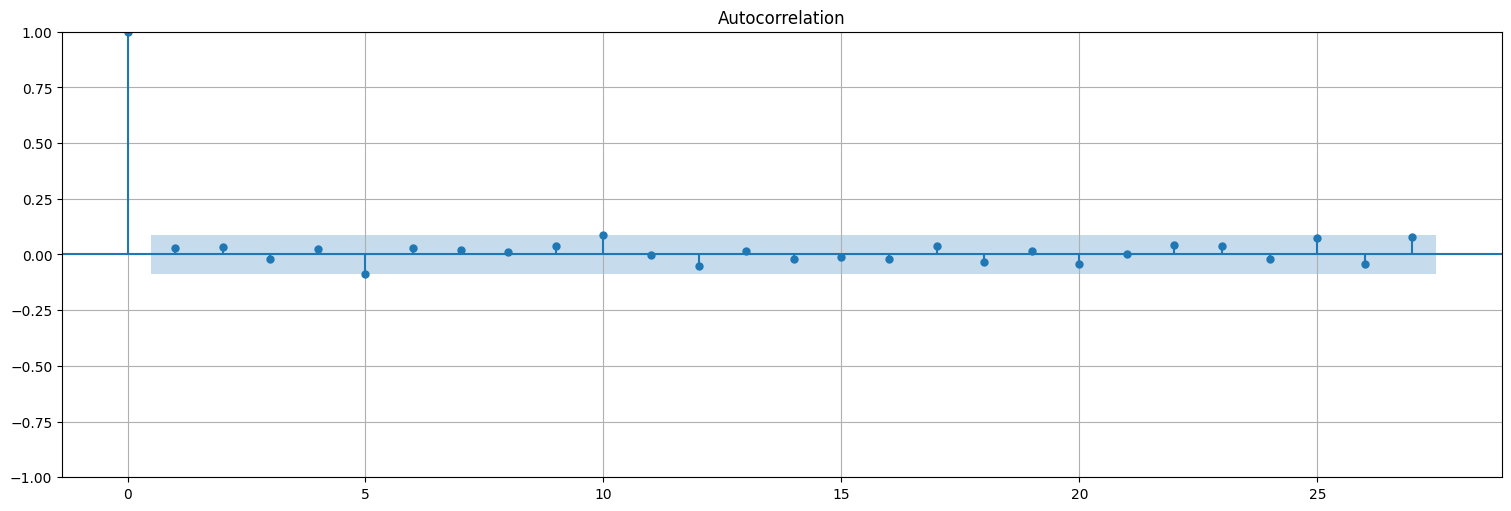
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
plot_acf(w, bartlett_confint=False);
Modelos autorregresivos¶
Definición: un proceso autorregresivo de orden \(p\) es un proceso en el cual el valor en tiempo \(t\) es una combinación lineal de los últimos \(p\) valores de la serie, más una innovación o ruido que afecta solo al tiempo \(t\):
con \(x_0,\ldots,x_{p-1}\) especificados y \(w_t\) ruido blanco (gaussiano) de varianza \(\sigma_w^2\).
Parametrización alternativa:
Otra forma de escribir el mismo proceso es
con \(a_0=1\), \(a_i = -\phi_i\), \(b_0=\sigma_w\) y en este caso \(w_t\) es ruido blanco de varianza \(1\). Esta es la parametrización que se utiliza en Python.
Ejemplo:¶
Consideremos el proceso:
o bien
Con \(x_{0}\) y \(x_{-1}\) dados (por ejemplo 0) y \(\sigma_w^2=1\).
Este es un proceso autorregresivo de orden 2. En este caso \(a=(1,-1,0.9)\) y \(b_0=\sigma_w = 1\).
Para simular una realización en Python podemos:
Generarlo a partir de una muestra de ruido blanco como la anterior, usando la función
lfilterdescipy.signalcomoscipy.signal.lfilter(b, a, x).Generarlo directamente a partir de un objeto de tipo
statsmodels.tsa.ArmaProcess.
from scipy.signal import lfilter
x = lfilter([1],[1,-1,0.9],w)
plt.plot(x)
plt.title("Proceso autorregresivo de orden 2");
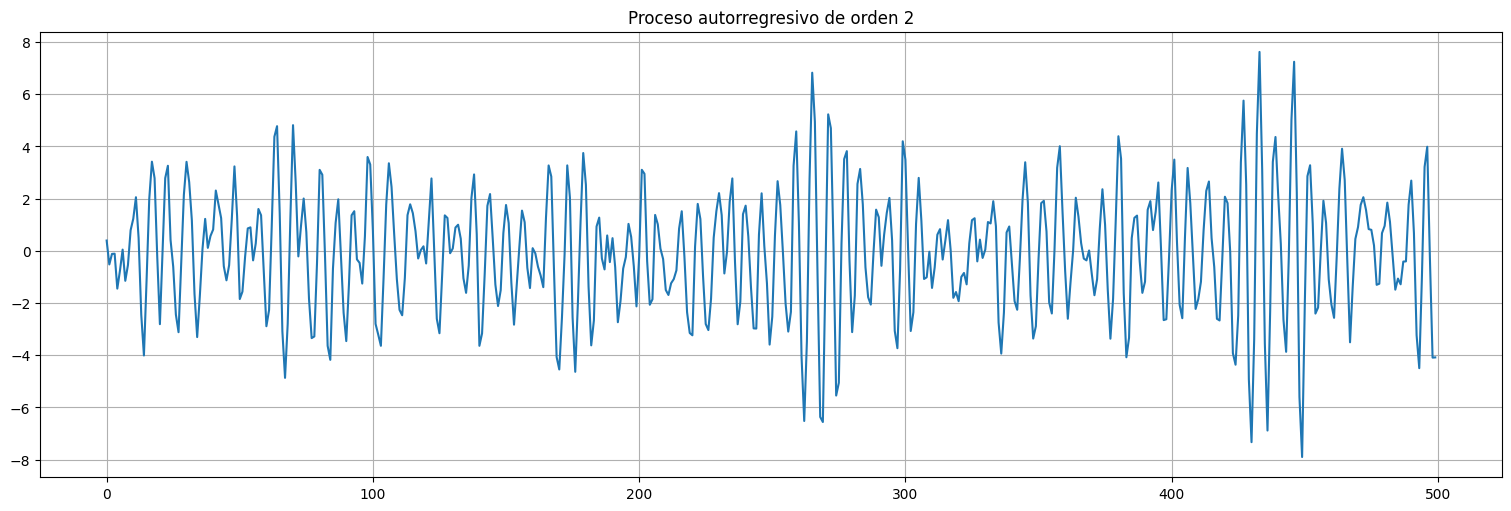
Autocorrelación del proceso:¶
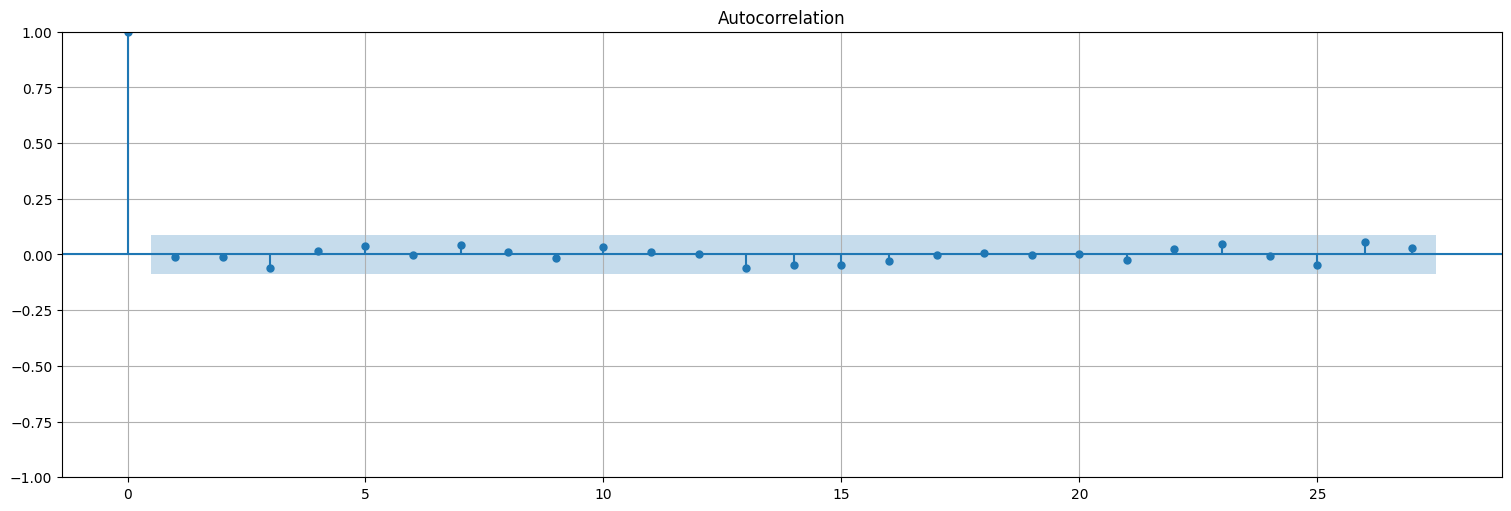
Uno tiende a pensar que la autocorrelación del proceso solo tendrá valores significativos para los 2 anteriores. FALSO
plot_acf(x, bartlett_confint=False);
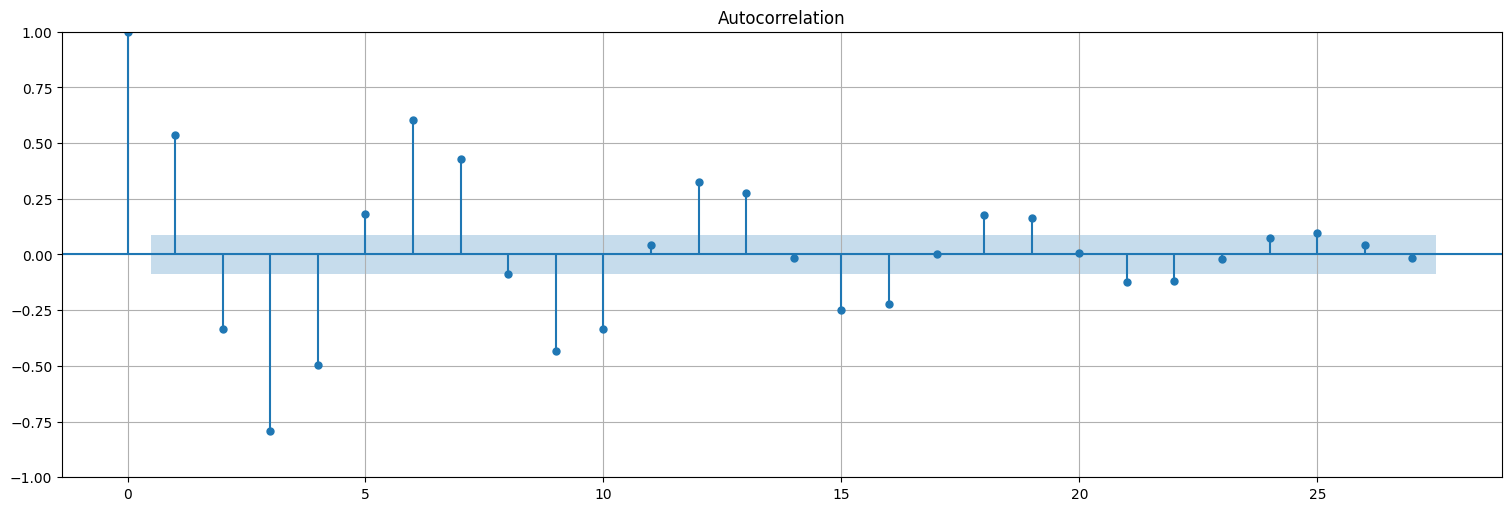
Ejemplo: autorregresivo de orden 1¶
Consideremos el proceso: $\(x_t = 0.9 x_{t-1} + w_t.\)$
Con \(x_{0}\) dado (por ejemplo 0).
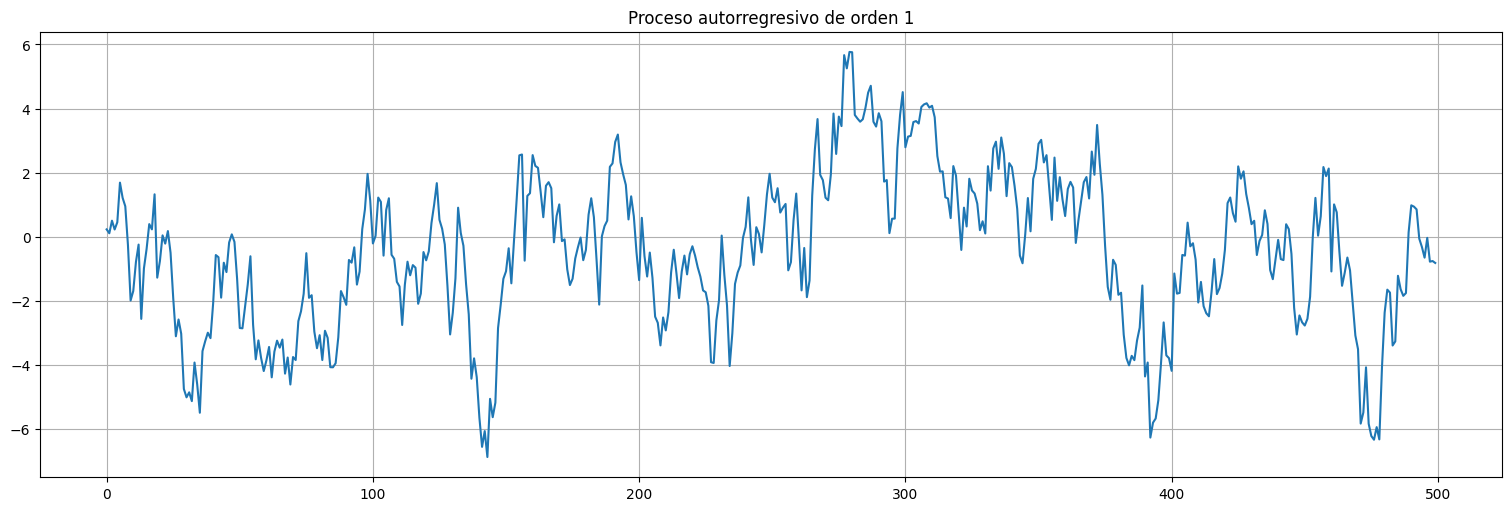
Este es un proceso autorregresivo de orden 1. Cada muestra recuerda a la anterior.
w = np.random.normal(loc=0,scale=1,size=500)
x = lfilter([1], [1,-0.9],w)
plt.plot(x)
plt.title("Proceso autorregresivo de orden 1");
plot_acf(x, bartlett_confint=False);
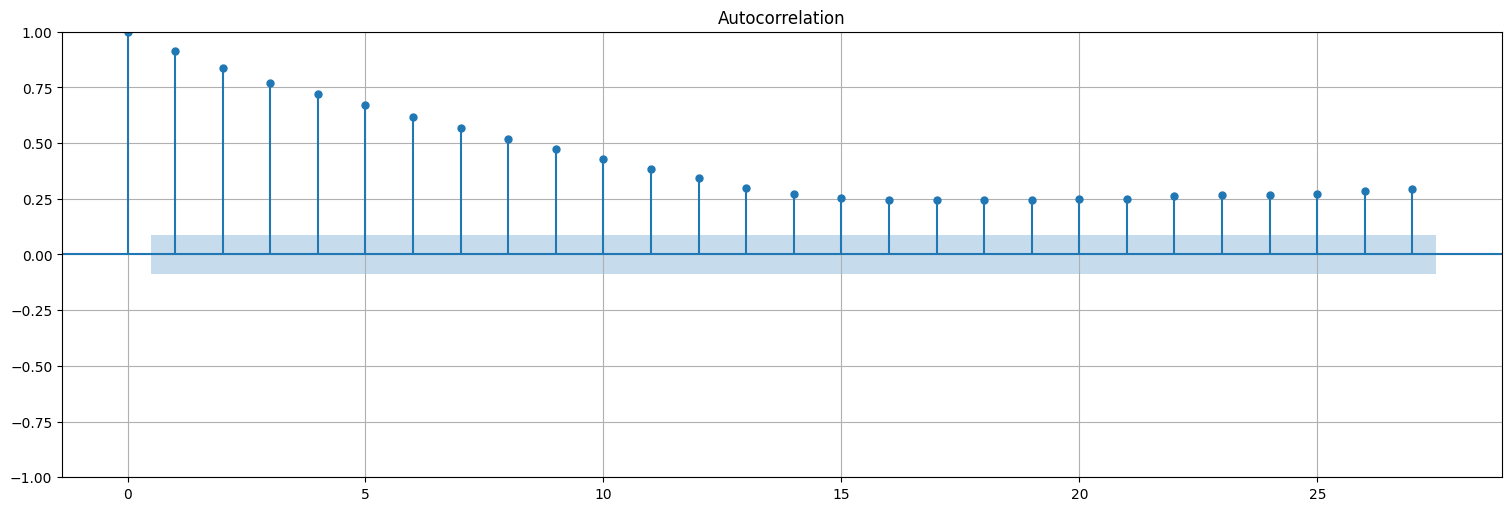
Pregunta: ¿Cómo podemos determinar el orden de un proceso de este tipo? ¿Cómo podemos determinar sus parámetros?
Ajuste de modelos autorregresivos.¶
Estimación de un AR(1)¶
Supongamos que sabemos que el orden es conocido. Por ejemplo, para este caso, de orden \(1\).
Probemos mirar la correlación entre un valor y el anterior:
#Este comando de pandas plotea x_t vs x_t-1
x=pd.Series(x) #transformo x en una serie temporal
pd.plotting.lag_plot(x,lag=1);
plt.title(f"Coeficiente de correlación: {x.autocorr(1)}");
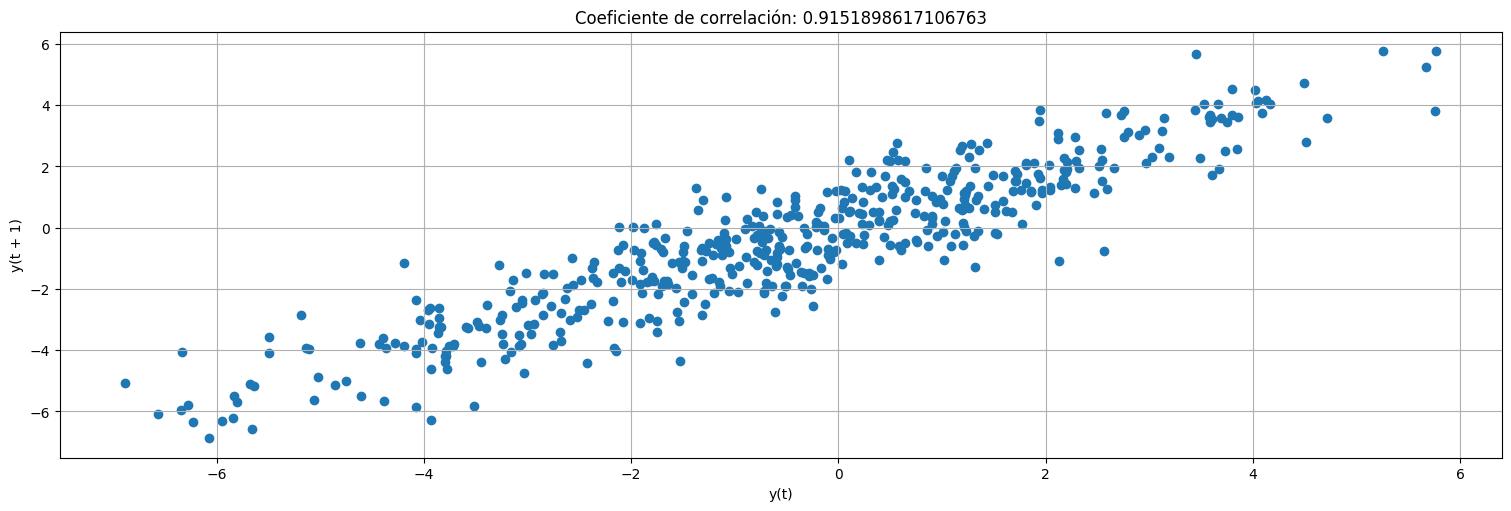
Más precisamente, podemos ajustar un modelo lineal entre los datos de la serie \(x_t\) y la serie “laggeada”:
from statsmodels.formula.api import ols
#Podemos llamar a fit haciendo referencia a las columnas de un dataframe.
data = pd.concat([x, x.shift(1)], axis=1).dropna()
data.columns = ["x", "xL1"]
fit = ols("x ~ 0+xL1", data=data).fit()
print(f"MSE de los residuos: {fit.mse_resid}")
fit.summary()
MSE de los residuos: 0.9355830439467617
| Dep. Variable: | x | R-squared (uncentered): | 0.844 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.844 |
| Method: | Least Squares | F-statistic: | 2694. |
| Date: | Mon, 19 May 2025 | Prob (F-statistic): | 4.74e-203 |
| Time: | 16:18:19 | Log-Likelihood: | -690.94 |
| No. Observations: | 499 | AIC: | 1384. |
| Df Residuals: | 498 | BIC: | 1388. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| xL1 | 0.9188 | 0.018 | 51.907 | 0.000 | 0.884 | 0.954 |
| Omnibus: | 1.192 | Durbin-Watson: | 2.017 |
|---|---|---|---|
| Prob(Omnibus): | 0.551 | Jarque-Bera (JB): | 1.012 |
| Skew: | -0.097 | Prob(JB): | 0.603 |
| Kurtosis: | 3.106 | Cond. No. | 1.00 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
#Miramos los residuos del ajuste
residuos = fit.resid
plot_acf(residuos, bartlett_confint=False);
Probemos ahora con el AR(2)¶
x = lfilter([1],[1,-1,0.9],w)
plt.plot(x)
plt.title("Proceso autorregresivo de orden 2");
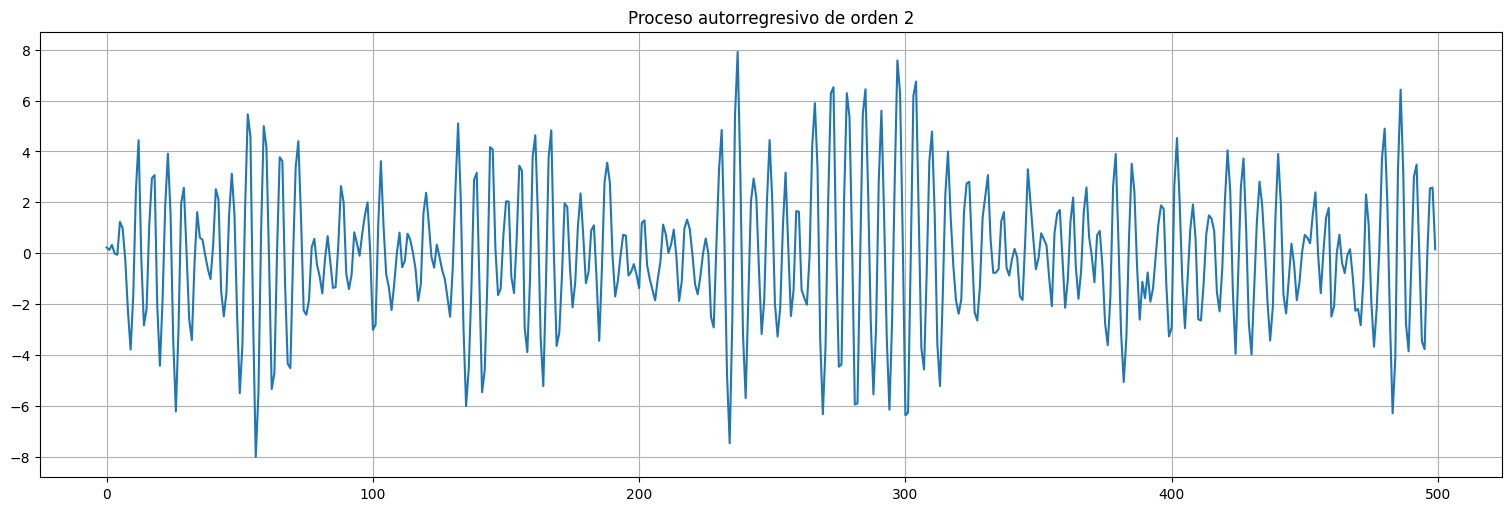
Correlaciones con los dos lags anteriores:
x=pd.Series(x) #transformo x en una serie temporal
pd.plotting.lag_plot(x,lag=1);
plt.title(f"Coeficiente de correlación: {x.autocorr(1)}");
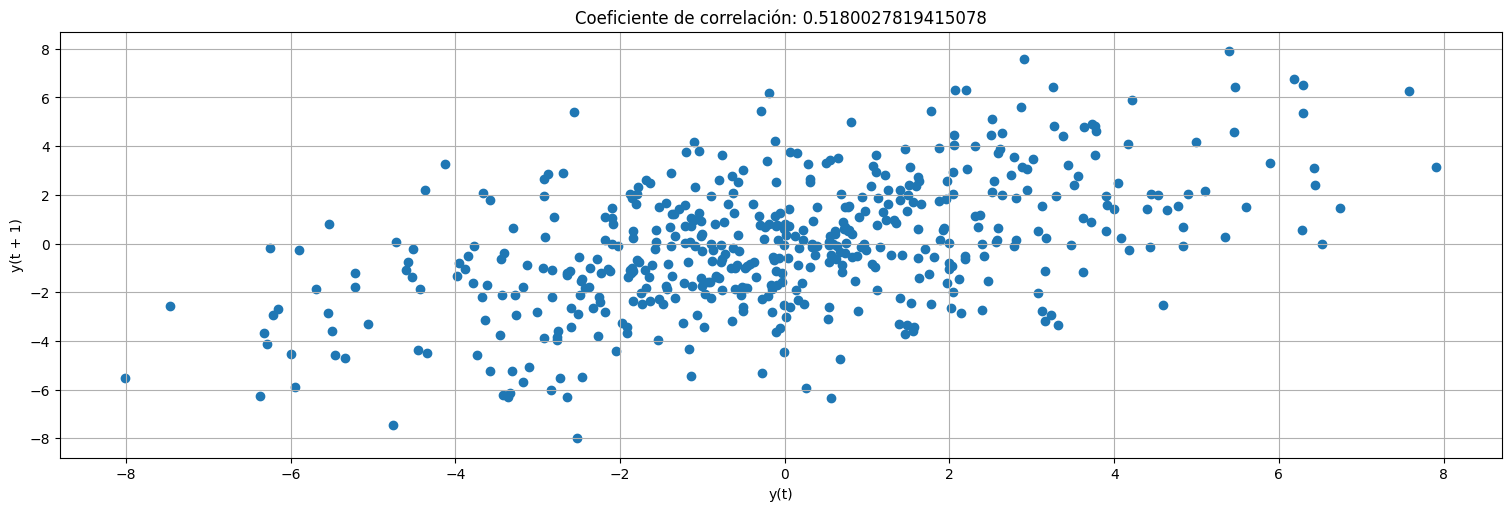
pd.plotting.lag_plot(x,lag=2);
plt.title(f"Coeficiente de correlación: {x.autocorr(2)}");
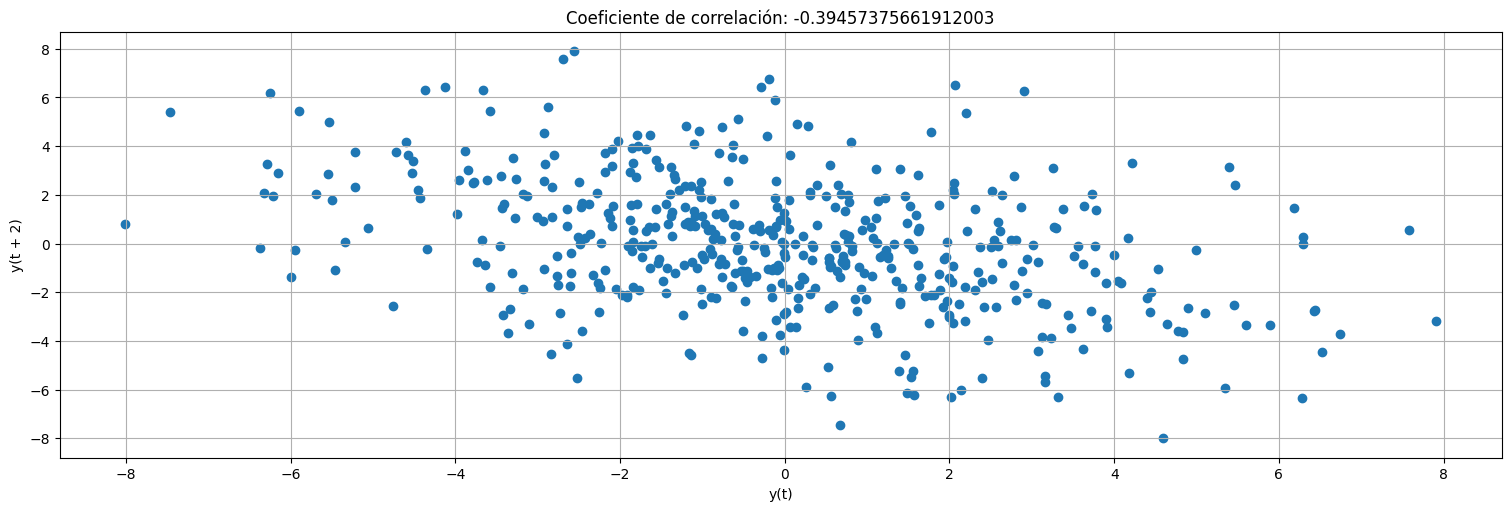
Nuevamente, ajustamos por mínimos cuadrados un modelo lineal a la serie \(x_t\) en función de los dos lags anteriores:
x=pd.Series(x)
data = pd.concat([x, x.shift(1), x.shift(2)], axis=1).dropna()
data.columns = ["x", "xL1", "xL2"]
fit = ols("x ~ 0+xL1+xL2", data=data).fit()
print(f"MSE de los residuos: {fit.mse_resid}")
fit.summary()
MSE de los residuos: 0.9394490858244653
| Dep. Variable: | x | R-squared (uncentered): | 0.869 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.869 |
| Method: | Least Squares | F-statistic: | 1648. |
| Date: | Mon, 19 May 2025 | Prob (F-statistic): | 8.18e-220 |
| Time: | 16:18:20 | Log-Likelihood: | -690.08 |
| No. Observations: | 498 | AIC: | 1384. |
| Df Residuals: | 496 | BIC: | 1393. |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| xL1 | 0.9882 | 0.019 | 52.035 | 0.000 | 0.951 | 1.026 |
| xL2 | -0.9073 | 0.019 | -47.728 | 0.000 | -0.945 | -0.870 |
| Omnibus: | 1.013 | Durbin-Watson: | 1.953 |
|---|---|---|---|
| Prob(Omnibus): | 0.603 | Jarque-Bera (JB): | 0.862 |
| Skew: | -0.094 | Prob(JB): | 0.650 |
| Kurtosis: | 3.079 | Cond. No. | 1.78 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Los residuos quedan sin autocorrelación (ruido blanco):
plot_acf(fit.resid, bartlett_confint=False);
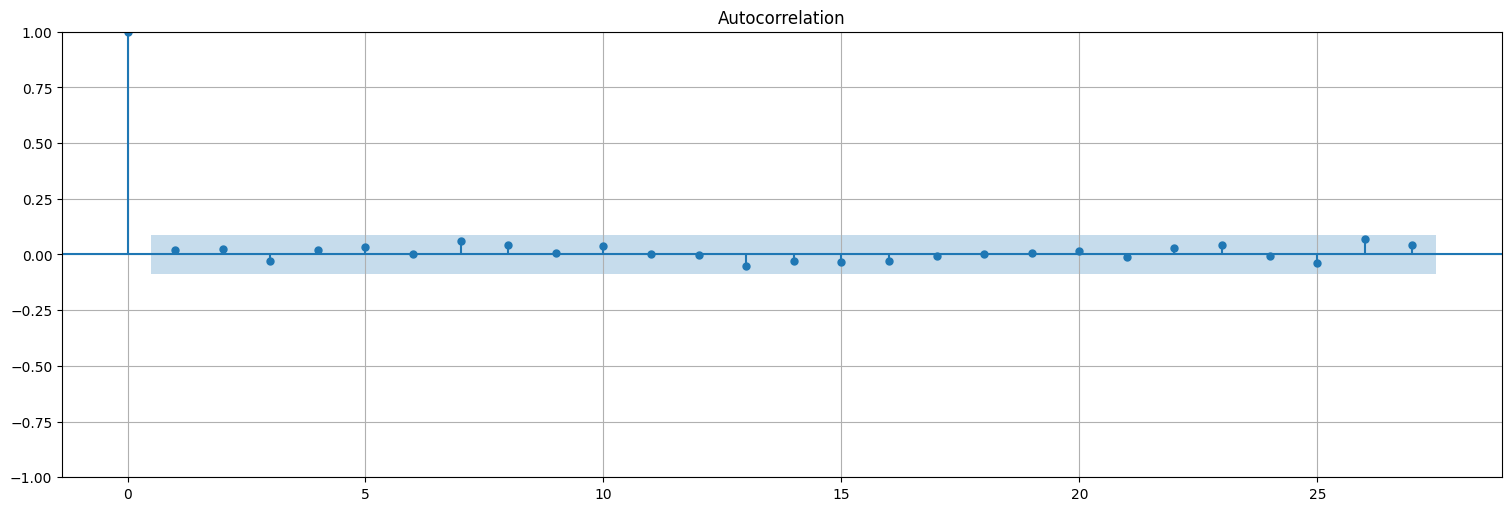
Podemos ver además que los residuos siguen una distribución gaussiana:
from statsmodels.graphics.api import qqplot
qqplot(fit.resid,line='s');
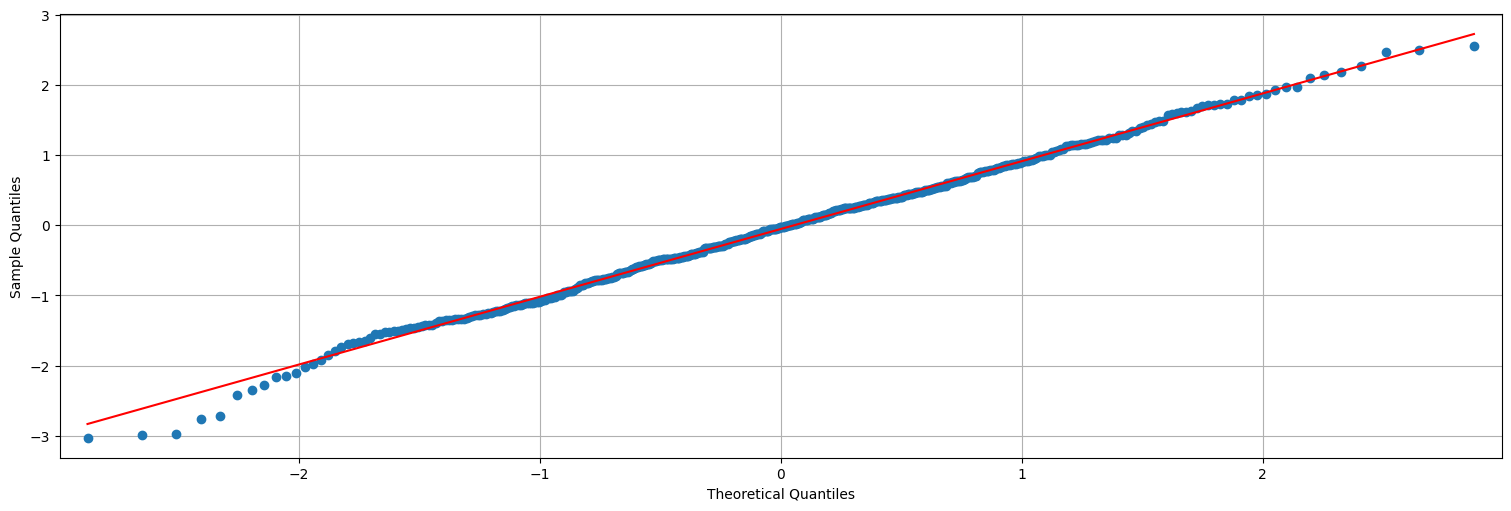
De hecho, si el ajuste es bueno, los residuos del ajuste deberían parecerse al ruido blanco que dio origen a la serie:
plt.plot(fit.resid, color="teal")
plt.scatter(fit.resid.index, w[2:], color="blue");
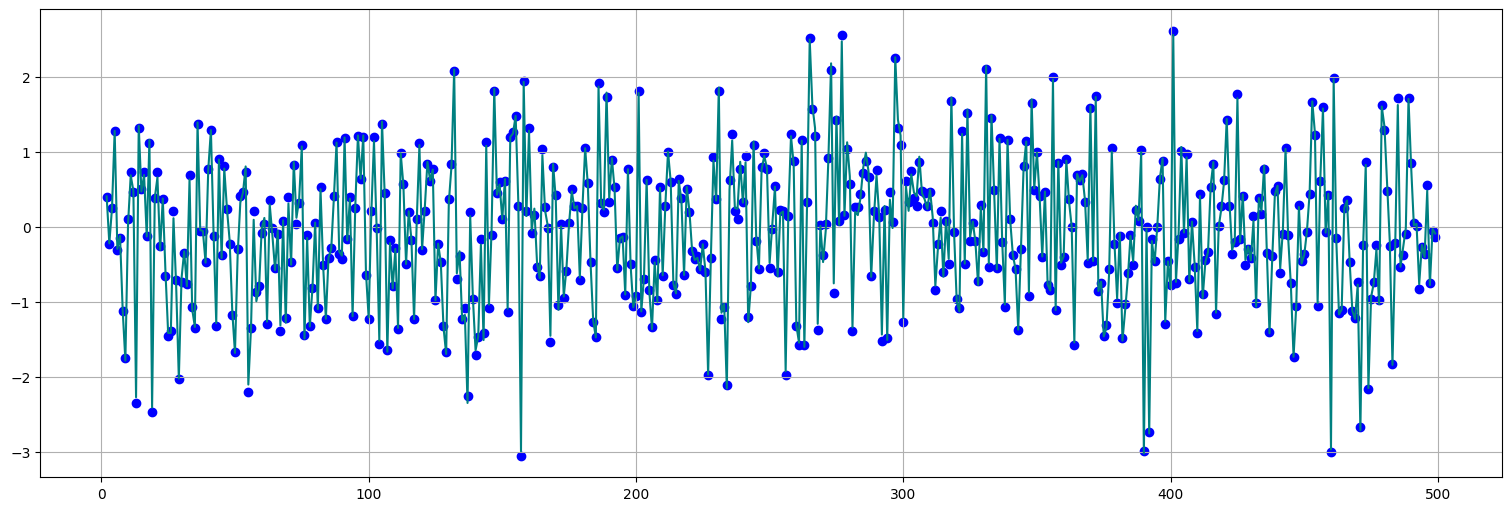
Conclusiones:¶
En un modelo AR(p), cada muestra depende del ruido actual y de una combinación lineal de las observaciones anteriores
La autocorrelación de todos modos depende de todas las muestras que vinieron antes!
Si conocemos el orden del modelo, podemos hacer una regresión lineal para explicar \(x_t\) a partir de \(x_{t-1}\) hasta \(x_{t-p}\). De ese modo se obtienen los valores de los coeficientes. Pregunta: ¿Cuál es el orden adecuado?
Si el proceso ajusta, los residuos deberían ser aproximadamente ruido blanco y parecerse al ruido que dio origen a la serie.
Función de autocorrelación parcial (PACF)¶
Idea: construir una función de correlación que solo contenga los aportes “incrementales” de agregar un lag, y no la correlación completa.
Se explica mejor a través de un ejemplo, dejaremos la teoría para más adelante.
Retomemos la serie:
Recordemos la función de autocorrelación (ACF)
plot_acf(x, bartlett_confint=False);
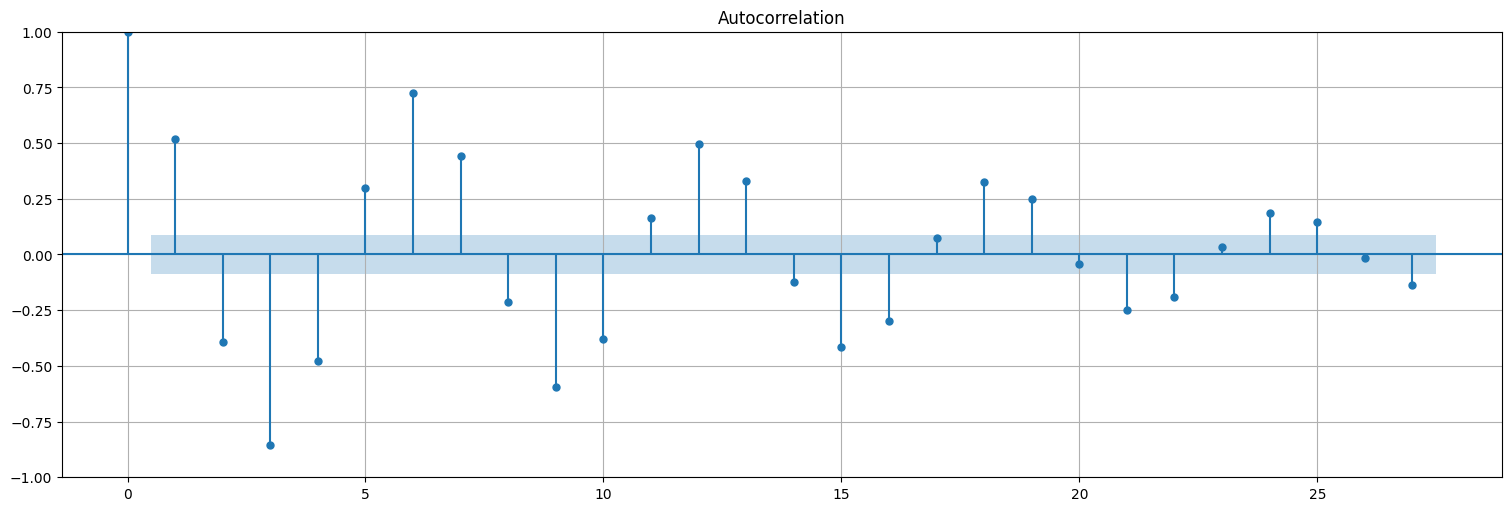
Paso 1: Ajustamos \(x_t\) a \(x_{t-1}\):
#Corto la serie x con la serie x laggeada
data = pd.concat([x, x.shift(1)], axis=1).dropna()
data.columns = ["x", "xL1"]
#Ajusto
fit = ols("x ~ 0+xL1", data=data).fit()
fit.summary() #el coef. hallado es la correlación de xt y xt-1, es decir acf(1)
| Dep. Variable: | x | R-squared (uncentered): | 0.269 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.267 |
| Method: | Least Squares | F-statistic: | 182.8 |
| Date: | Mon, 19 May 2025 | Prob (F-statistic): | 1.05e-35 |
| Time: | 16:18:20 | Log-Likelihood: | -1120.5 |
| No. Observations: | 499 | AIC: | 2243. |
| Df Residuals: | 498 | BIC: | 2247. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| xL1 | 0.5182 | 0.038 | 13.521 | 0.000 | 0.443 | 0.593 |
| Omnibus: | 0.037 | Durbin-Watson: | 1.061 |
|---|---|---|---|
| Prob(Omnibus): | 0.982 | Jarque-Bera (JB): | 0.018 |
| Skew: | 0.014 | Prob(JB): | 0.991 |
| Kurtosis: | 2.996 | Cond. No. | 1.00 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
pd.plotting.lag_plot(x,lag=1);
plt.plot(x[0:-1],fit.fittedvalues);
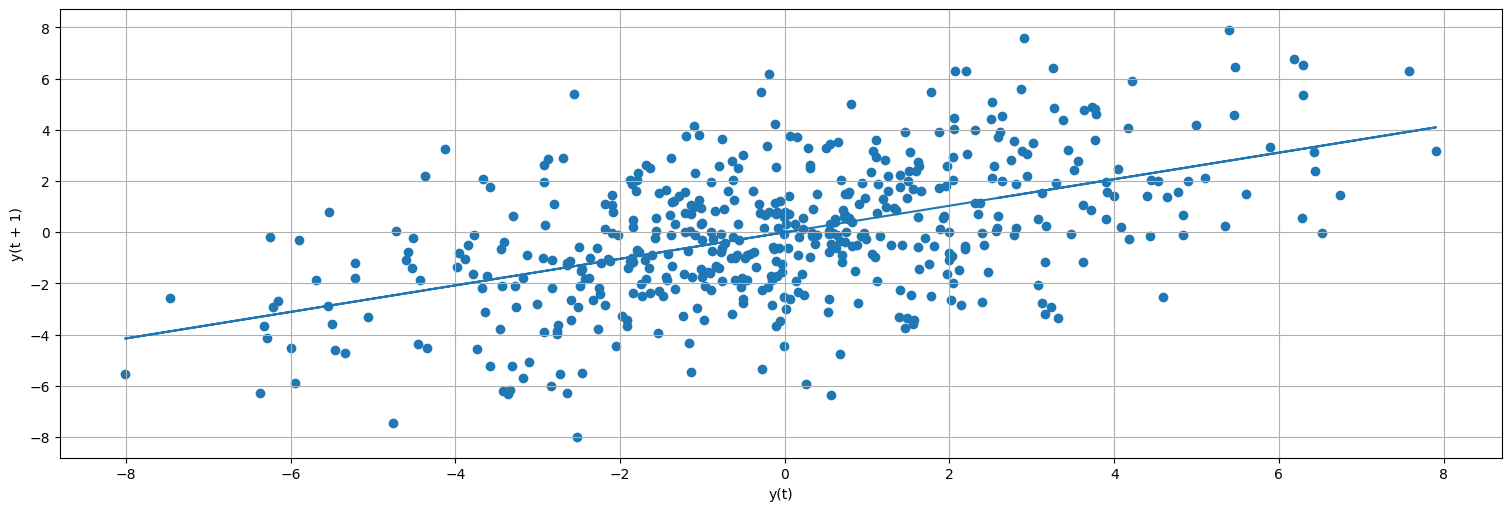
#capturo los residuos del ajuste anterior
r1 = fit.resid
r1.plot();
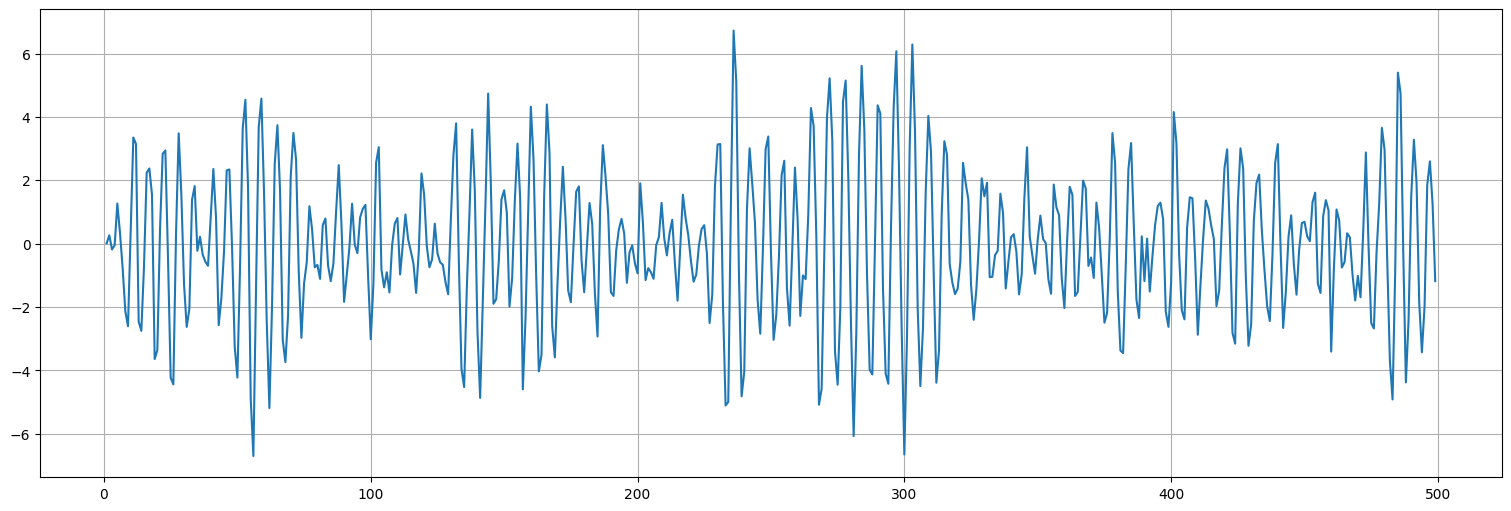
Si el proceso fuera de orden \(1\), entonces una vez que conozco \(x_{t-1}\), \(x_t\) queda determinado a menos del ruido, por lo que el residuo no debería tener información.
La serie anterior todavía no está del todo “blanca” quiere decir que debemos seguir un paso más.
Problema: no alcanza con mirar otro lag, debemos “extraer” la información de \(x_{t-2}\) que persiste en \(x_t\).
Para ello, miramos los residuos de los dos ajustes siguientes:
Ajusto \(x_t\) a \(x_{t-1}\), obtengo \(r_1\) (es el mismo de antes).
Ajusto \(x_{t-2}\) a \(x_{t-1}\) para extraer la info propia de \(x_{t-2}\). Obtengo \(r_2\).
Calculo la correlación entre \(r_1\) y \(r_2\) (o bien ajusto lineal \(r_2\) a \(r_1\), es lo mismo). Al resultado se le llama autocorrelación parcial entre \(x_t\) y \(x_{t-2}\) (o de lag 2).
#Realizo el procedimiento anterior
data = pd.concat([x, x.shift(1), x.shift(2)], axis=1).dropna()
data.columns = ["x", "xL1", "xL2"]
#Ajusto r1
fit1 = ols("x ~ 0+xL1", data=data).fit()
r1=fit1.resid
fit1.summary() #el coef. hallado es la correlación de xt y xt-1, es decir acf(1)
| Dep. Variable: | x | R-squared (uncentered): | 0.269 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.267 |
| Method: | Least Squares | F-statistic: | 182.4 |
| Date: | Mon, 19 May 2025 | Prob (F-statistic): | 1.24e-35 |
| Time: | 16:18:21 | Log-Likelihood: | -1118.7 |
| No. Observations: | 498 | AIC: | 2239. |
| Df Residuals: | 497 | BIC: | 2244. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| xL1 | 0.5182 | 0.038 | 13.507 | 0.000 | 0.443 | 0.594 |
| Omnibus: | 0.030 | Durbin-Watson: | 1.061 |
|---|---|---|---|
| Prob(Omnibus): | 0.985 | Jarque-Bera (JB): | 0.020 |
| Skew: | 0.015 | Prob(JB): | 0.990 |
| Kurtosis: | 2.990 | Cond. No. | 1.00 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
#Ajusto r2
fit2 = ols("xL2 ~ 0+xL1", data=data).fit()
r2=fit2.resid
fit2.summary() #el coef. hallado es la correlación de xt y xt-1, es decir acf(1)
| Dep. Variable: | xL2 | R-squared (uncentered): | 0.269 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.267 |
| Method: | Least Squares | F-statistic: | 182.8 |
| Date: | Mon, 19 May 2025 | Prob (F-statistic): | 1.08e-35 |
| Time: | 16:18:21 | Log-Likelihood: | -1118.1 |
| No. Observations: | 498 | AIC: | 2238. |
| Df Residuals: | 497 | BIC: | 2242. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| xL1 | 0.5181 | 0.038 | 13.520 | 0.000 | 0.443 | 0.593 |
| Omnibus: | 0.586 | Durbin-Watson: | 1.062 |
|---|---|---|---|
| Prob(Omnibus): | 0.746 | Jarque-Bera (JB): | 0.425 |
| Skew: | 0.051 | Prob(JB): | 0.809 |
| Kurtosis: | 3.100 | Cond. No. | 1.00 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
plt.scatter(r1,r2);
plt.title(f"Correlación remanente: {np.corrcoef(r1,r2)[0,1]}");
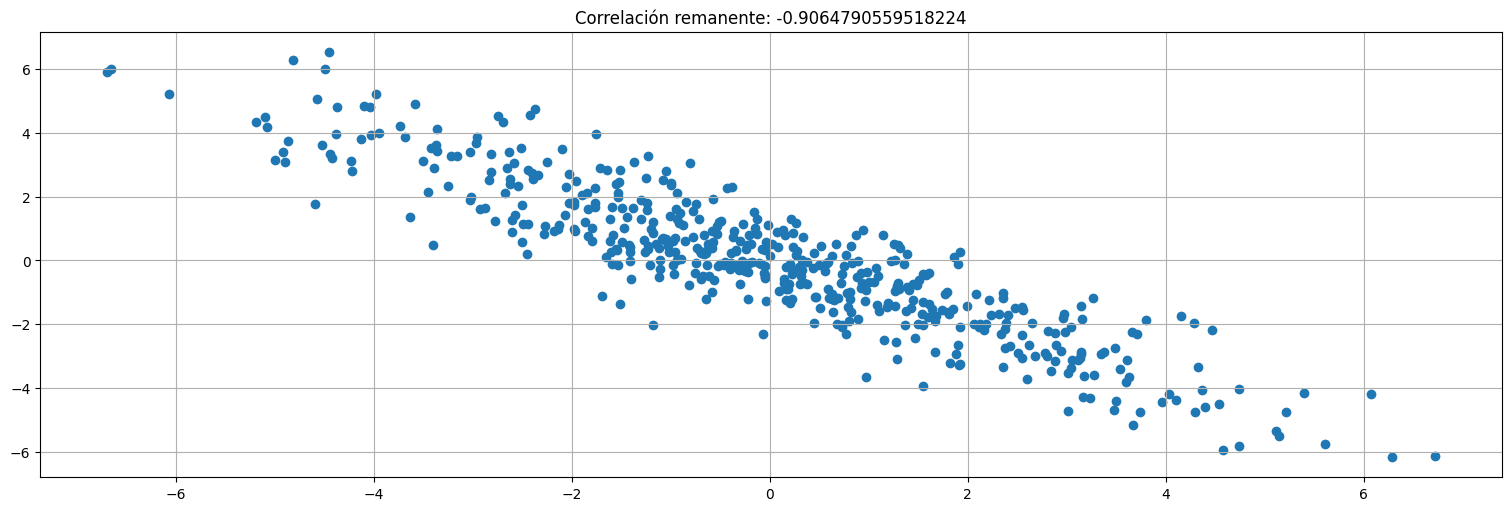
El método anterior puede repetirse para todos los lags. Simplemente:
Ajusto \(x_t\) a \(x_{t-1},\ldots,x_{t-p+1}\), obtengo \(r_1\).
Ajusto \(x_{t-p}\) a \(x_{t-1},\ldots,x_{t-p+1}\), obtengo \(r_2\).
Calculo la correlación entre \(r_1\) y \(r_2\) (o bien ajusto lineal \(r_2\) a \(r_1\), es lo mismo). Al resultado se le llama autocorrelación parcial entre \(x_t\) y \(x_{t-p}\) (o de lag \(p\)).
Hagamoslo un paso más (\(p=3\)) para ver que ya no queda información.
#Realizo el procedimiento anterior
#Realizo el procedimiento anterior
data = pd.concat([x, x.shift(1), x.shift(2), x.shift(3)], axis=1).dropna()
data.columns = ["x", "xL1", "xL2", "xL3"]
#Ajusto r1
fit1 = ols("x ~ 0+xL1+xL2", data=data).fit()
r1=fit1.resid
#Ajusto r2
fit2 = ols("xL3 ~ 0+xL1+xL2", data=data).fit()
r2=fit2.resid
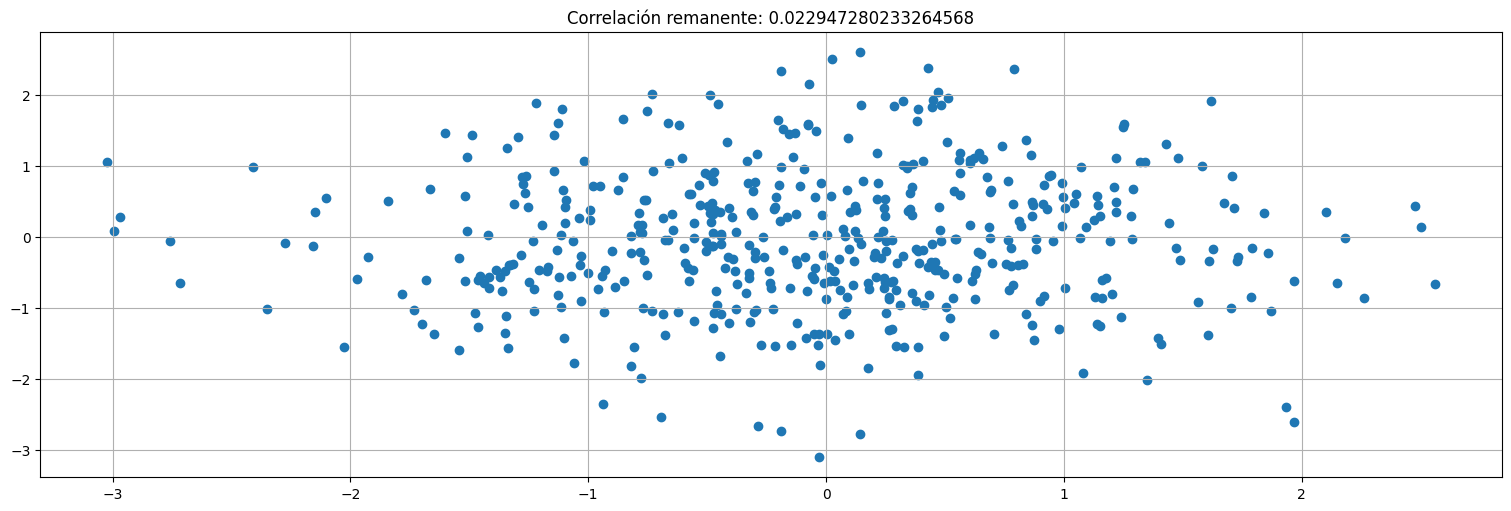
plt.scatter(r1,r2);
plt.title(f"Correlación remanente: {np.corrcoef(r1,r2)[0,1]}");
Función de autocorrelación parcial (PACF)¶
A la función así construida recursivamente se le denomina Función de Autocorrelación Parcial (PACF).
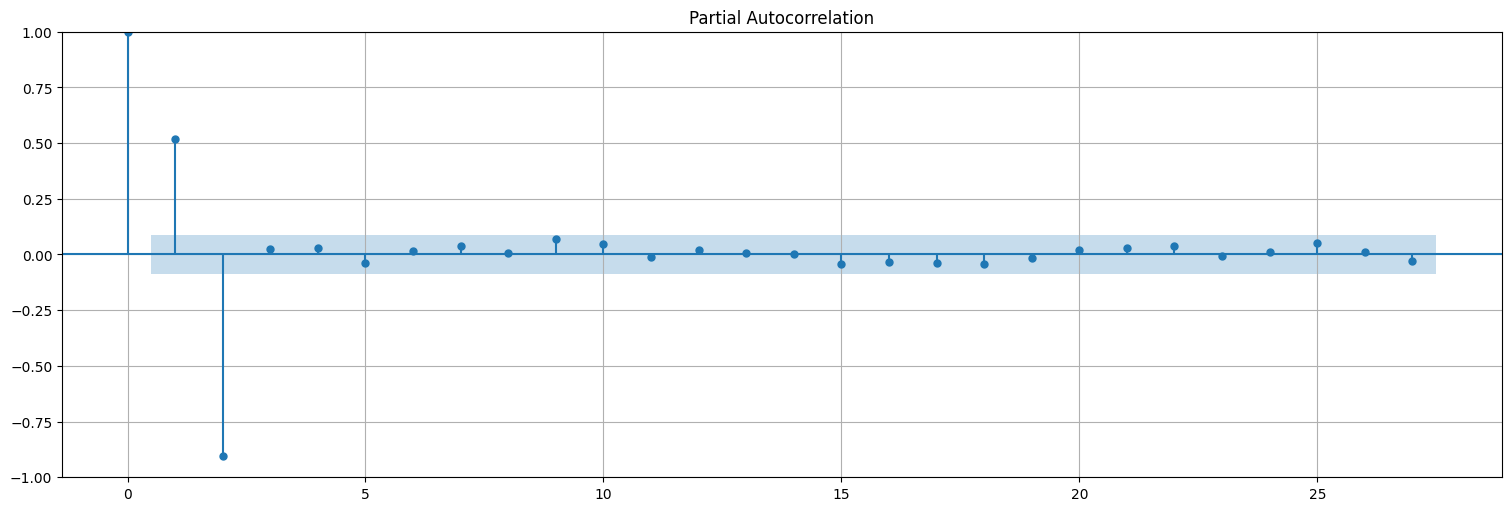
En el ejemplo anterior, la PACF(1) coincide con la ACF(1). La PACF(2) NO (es otra información).
En el proceso AR(2), la PACF(2) era significativa, la PACF(3) se vuelve 0.
En general, si un proceso es AR(\(p\)), entonces la PACF se “apaga” luego de \(p\).
plot_pacf(x);
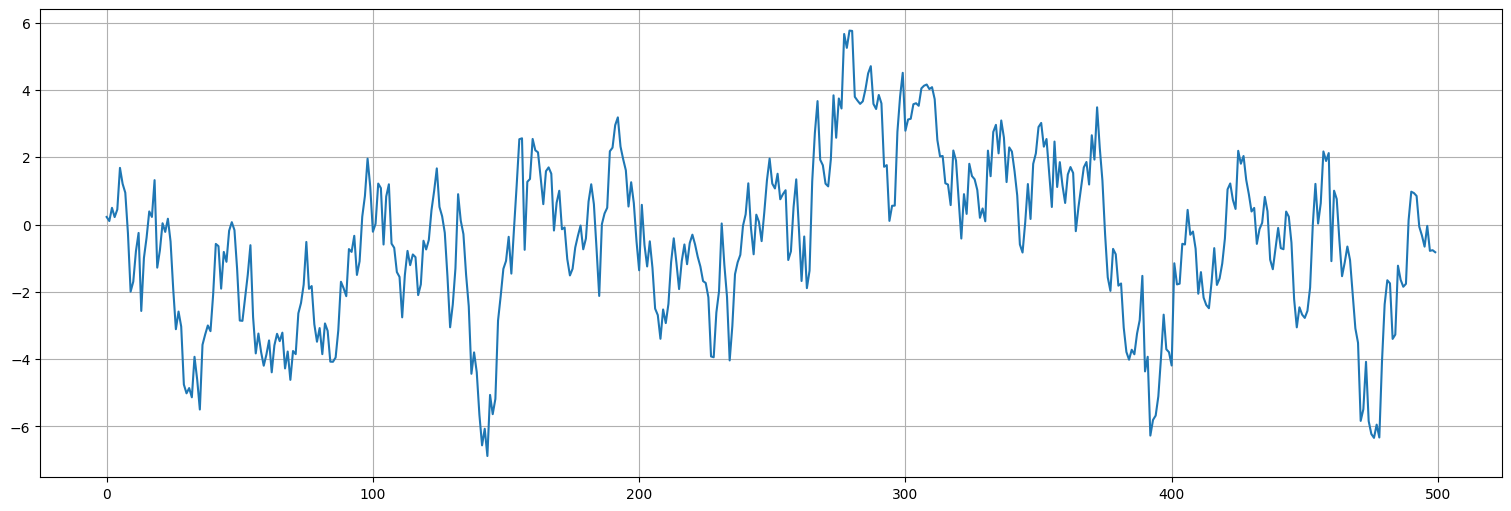
Apliquemos la misma idea al proceso AR(1) que teníamos antes
#esto se construye con el comando "filter" de R
x = lfilter([1],[1,-.9], w)
plt.plot(x);
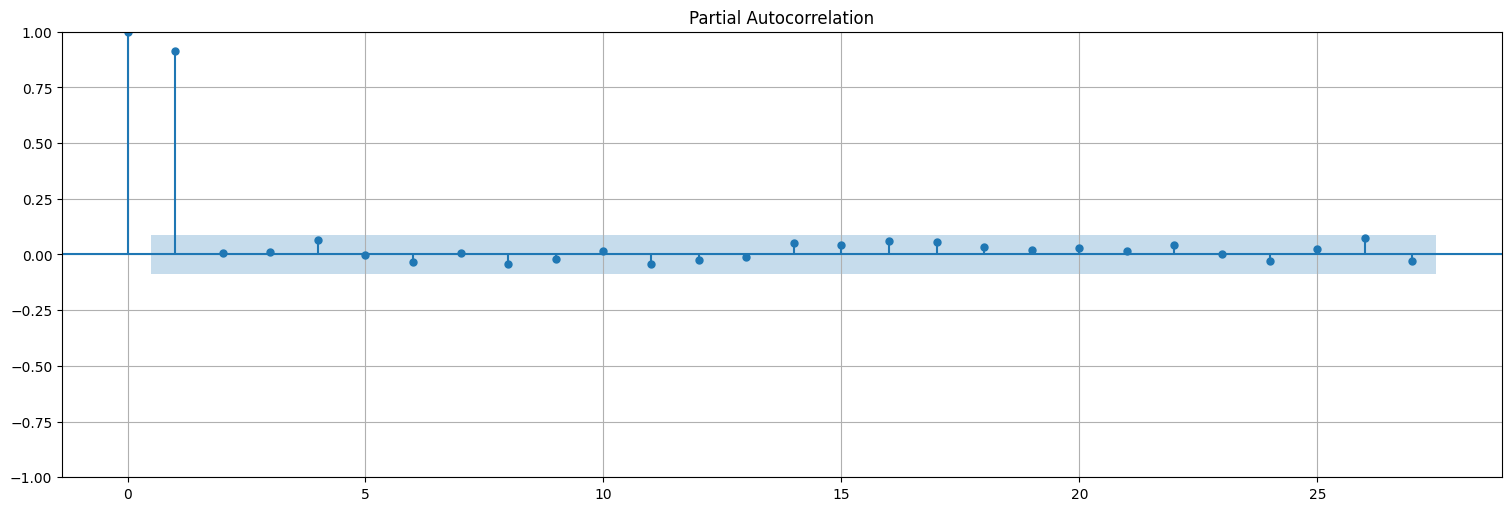
plot_acf(x,bartlett_confint=False);

plot_pacf(x);
Resumen¶
En un proceso autorregresivo puro, el valor de la serie en tiempo \(t\) depende de los \(p\) anteriores más una innovación o ruido en ese punto.
Por lo tanto, todas las muestras anteriores tienen influencia en la muestra actual (aunque decae exponencialmente).
La función de autocorrelación entonces decae a \(0\) exponencialmente, pero no se anula.
La función de autocorrelación parcial elimina las dependencias internas y permite estimar el orden de un autorregresivo puro.
Una vez que conocemos el orden, podemos hacer regresión para hallar los coeficientes y el \(\sigma^2_w\).
fit<- lm(x~xt1+xt2+xt3...)
Predicción a futuro¶
El siguiente paso es, una vez ajustado un proceso autorregresivo, predecir sus valores a futuro.
Idealmente, queremos hallar: $\(\hat{x}_{n+m} = g(x_1,\ldots,x_n)\)\( de modo que: \)\(MSE = E[(x_{n+m} - \hat{x}_{n+m})^2]\)$ se minimice.
El estimador ideal es la esperanza condicional:
En el caso de procesos lineales ARMA, este estimador se puede calcular mediante el algoritmo de Durbin-Levinson. Sin embargo, en el caso del autorregresivo puro es más simple. Una vez que se conocen los parámetros del modelo:
Entonces la mejor predicción de \(x_{p+1}\) es simplemente realizar la combinación lineal de los últimos \(p\) valores: $\(\hat{x}_{n+1} = \phi_1 x_{n} + \phi_2 x_{n-1} + \ldots + \phi_p x_{n-p+1}\)$
y luego recursivamemte se pueden construir las estimaciones de \(x_{n+2},x_{n+3},\ldots\) etc.
Ejemplo:¶
Para este ejemplo, simularemos directamente el proceso AR(2) usando una función de Python en lugar de construirlo a partir de una serie de ruido blanco conocida:
##Simulamos un AR(2) usando ahora la función propia de statsmodels
from statsmodels.tsa.arima_process import arma_generate_sample
#primer parámetro: coeficientes autorregresivos. Segundo parámetro: coeficientes de media móvil
#Para el AR puro este segundo parámetro es 1
#El tercer parámetro es la cantidad de muestras.
n=500; #train
m=20; #test
x=arma_generate_sample([1,-1,.9],[1],n+m)
#lo transformo en una serie para poder hacer shift
x=pd.Series(x)
x.plot();
Ajustamos los coeficientes con los primeros 500 datos y predecimos los otros 20.
## Recorto la serie
x_train = x.iloc[0:n]
## Chequeo la PACF
plot_pacf(x_train);
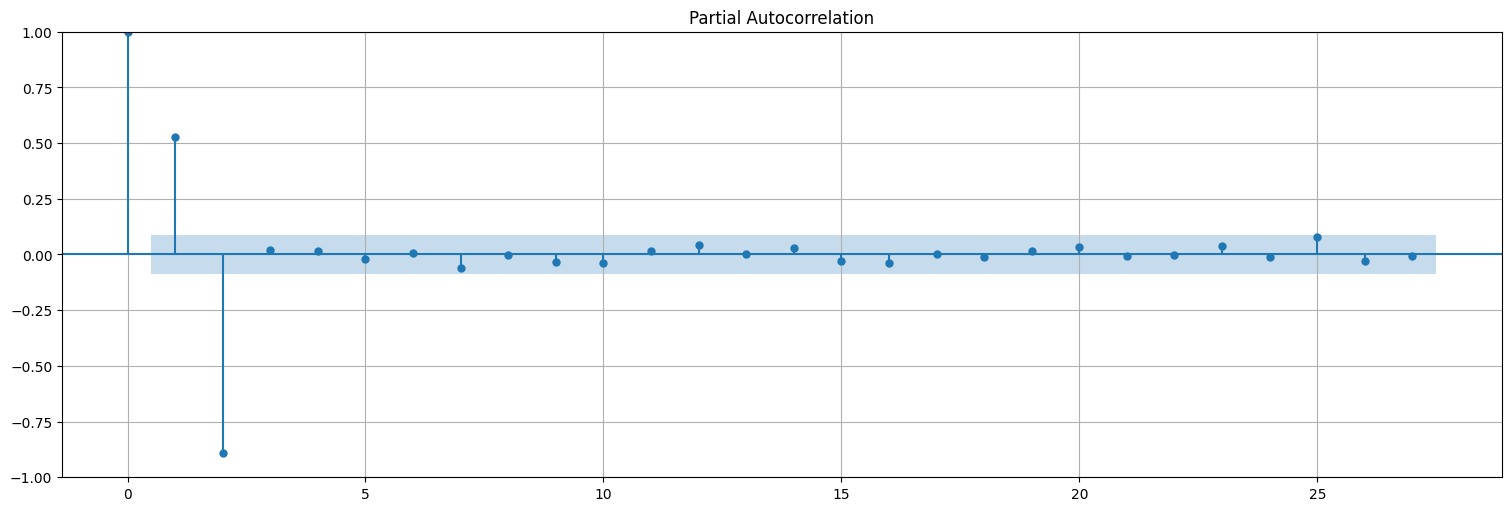
#Estimo los coeficientes por regresión en el conjunto de train
data = pd.concat([x_train, x_train.shift(1), x_train.shift(2)], axis=1).dropna()
data.columns = ["x", "xL1", "xL2"]
#Ajusto
fit = ols("x ~ 0+xL1+xL2", data=data).fit()
residuo=fit.resid
fit.summary() #el coef. hallado es la correlación de xt y xt-1, es decir acf(1)
| Dep. Variable: | x | R-squared (uncentered): | 0.854 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.854 |
| Method: | Least Squares | F-statistic: | 1455. |
| Date: | Mon, 19 May 2025 | Prob (F-statistic): | 2.96e-208 |
| Time: | 16:18:22 | Log-Likelihood: | -711.99 |
| No. Observations: | 498 | AIC: | 1428. |
| Df Residuals: | 496 | BIC: | 1436. |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| xL1 | 1.0011 | 0.020 | 49.568 | 0.000 | 0.961 | 1.041 |
| xL2 | -0.8950 | 0.020 | -44.238 | 0.000 | -0.935 | -0.855 |
| Omnibus: | 2.616 | Durbin-Watson: | 1.959 |
|---|---|---|---|
| Prob(Omnibus): | 0.270 | Jarque-Bera (JB): | 2.496 |
| Skew: | -0.106 | Prob(JB): | 0.287 |
| Kurtosis: | 3.274 | Cond. No. | 1.80 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
phi1 = fit.params["xL1"]
phi2 = fit.params["xL2"]
print("Coeficientes estimados:")
print(f"phi1: {phi1}")
print(f"phi2: {phi2}")
Coeficientes estimados:
phi1: 1.001125252883416
phi2: -0.8950251720111233
#Construyo la prediccion recursiva
x_test = x.iloc[n:]
x_hat = np.empty(m)
x_hat[0] = phi1 * x_train[n-1] + phi2*x_train[n-2]
x_hat[1] = phi1 * x_hat[0] + phi2*x_train[n-1]
for i in range(2,m):
x_hat[i] = phi1 * x_hat[i-1] + phi2*x_hat[i-2]
#lo convierto en una serie
x_hat = pd.Series(x_hat,index=range(n,n+m))
plt.plot(x_test, label="Valores de test")
plt.plot(x_hat, label="Prediccion");
plt.legend();
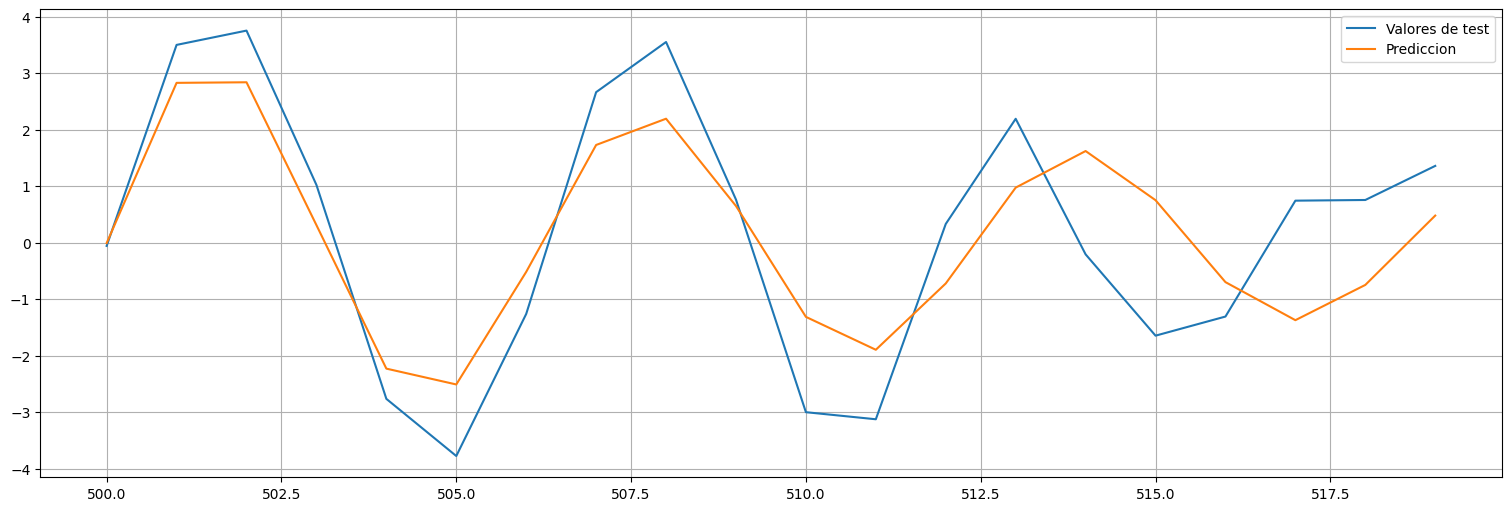
Observaciones:
La predicción solo es razonable a pocos intervalos.
A la larga vuelve a la media ya que promedia los valores que va obteniendo.
Dicho de otro modo, como la influencia de los datos hasta \(n\) decae exponencialmente después de \(n\), es muy difícil predecir más allá de unos pocos pasos.
Predicción recursiva¶
De todos modos, si bien no permite predecir mucho hacia el futuro, podemos ir recursivamente prediciendo el valor \(x_{n+1}\) una vez que conocemos \(x_{n},x_{n-1},\ldots,x_{n-p+1}\), es decir los últimos \(p\).
Luego si recibimos un dato nuevo podemos actualizar la predicción.
Ejemplo¶
##Simulamos un AR(2) usando la función propia de python
x=arma_generate_sample([1,-1,.9],[1],n)
x=pd.Series(x)
x.plot();
Supongamos que sabemos exactamente los parámetros, en este caso media \(\mu=0\), \(\phi_1=1.0\) y \(\phi_2=-0.9\).
Si solo predecimos por la media, el error MSE es el desvío estándar de la serie.
Si predecimos recursivamente \(x_{t+1}\) por \(\hat{x}_{t+1} = \phi_1 x_t + \phi_2 x_{t-1}\) entonces deberíamos poder reducir el error.
phi1 = 1.0
phi2 = -0.9
#aca va la predicción
x_hat = np.empty(n)
#los valores anteriores a t=0 los asumo 0 (la media)
x_hat[0] = phi1*0 + phi2*0
x_hat[1] = phi1 * x[0] + phi2*0
for i in range(2,n):
x_hat[i] = phi1 * x[i-1] + phi2*x[i-2]
#lo convierto en una serie
x_hat = pd.Series(x_hat)
x.plot()
x_hat.plot();
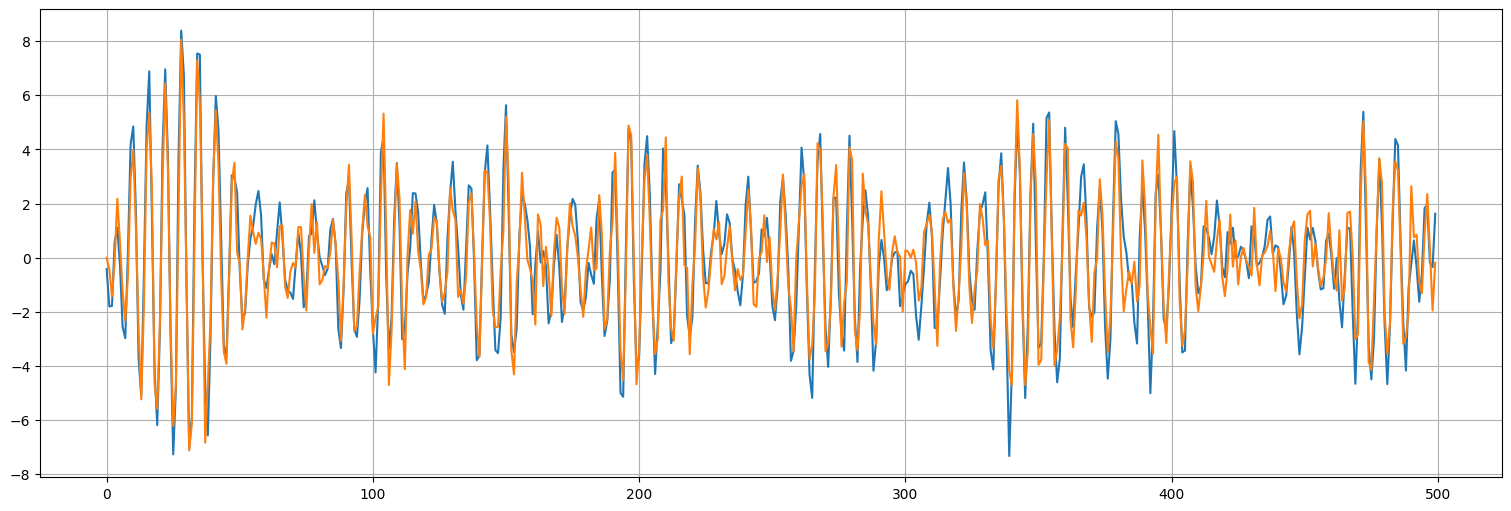
##Residuo
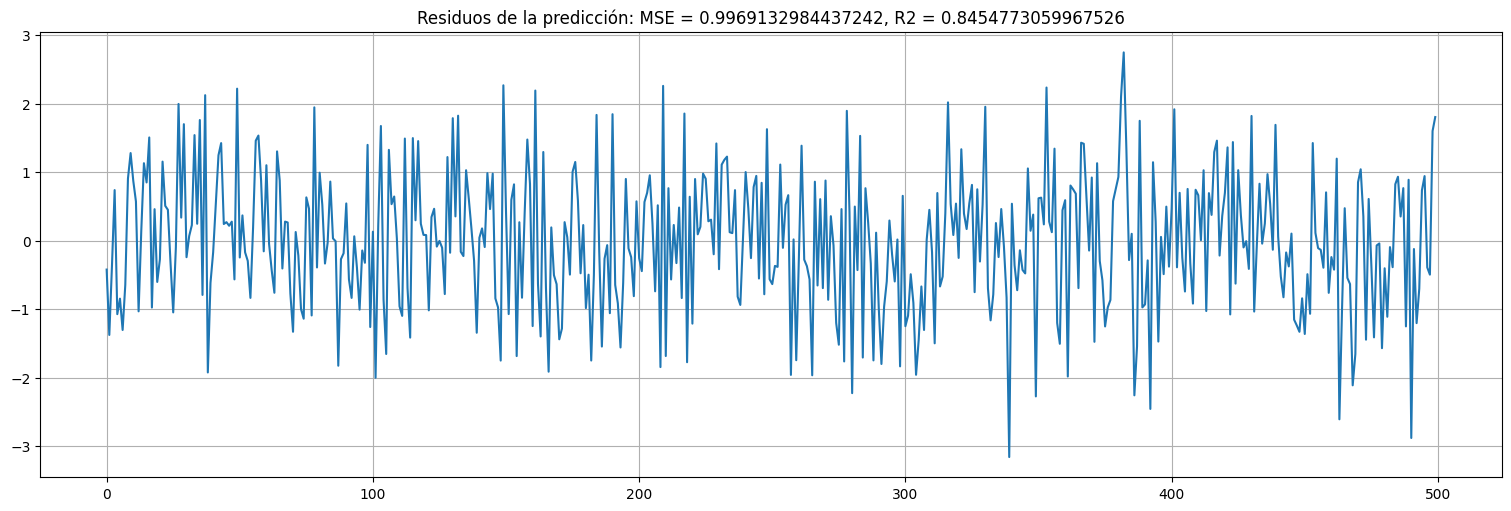
residuo = x-x_hat
MSE = np.var(residuo)
R2 = (np.var(x)-MSE)/np.var(x)
residuo.plot()
plt.title(f"Residuos de la predicción: MSE = {MSE}, R2 = {R2}");
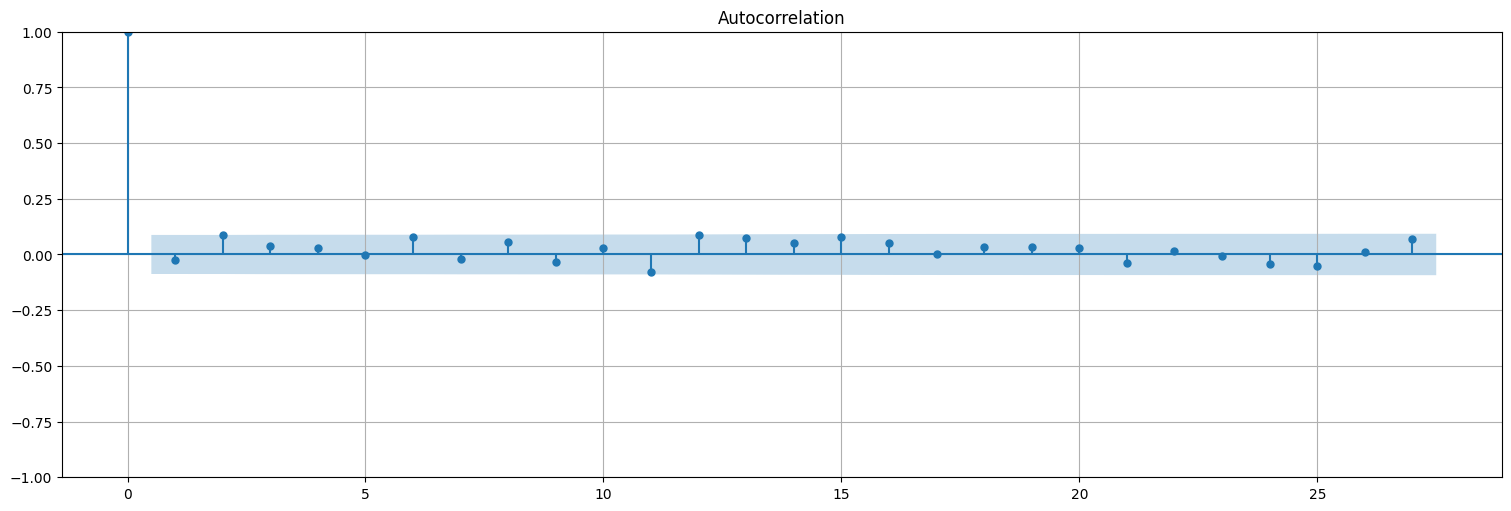
plot_acf(residuo);
Ejercicios¶
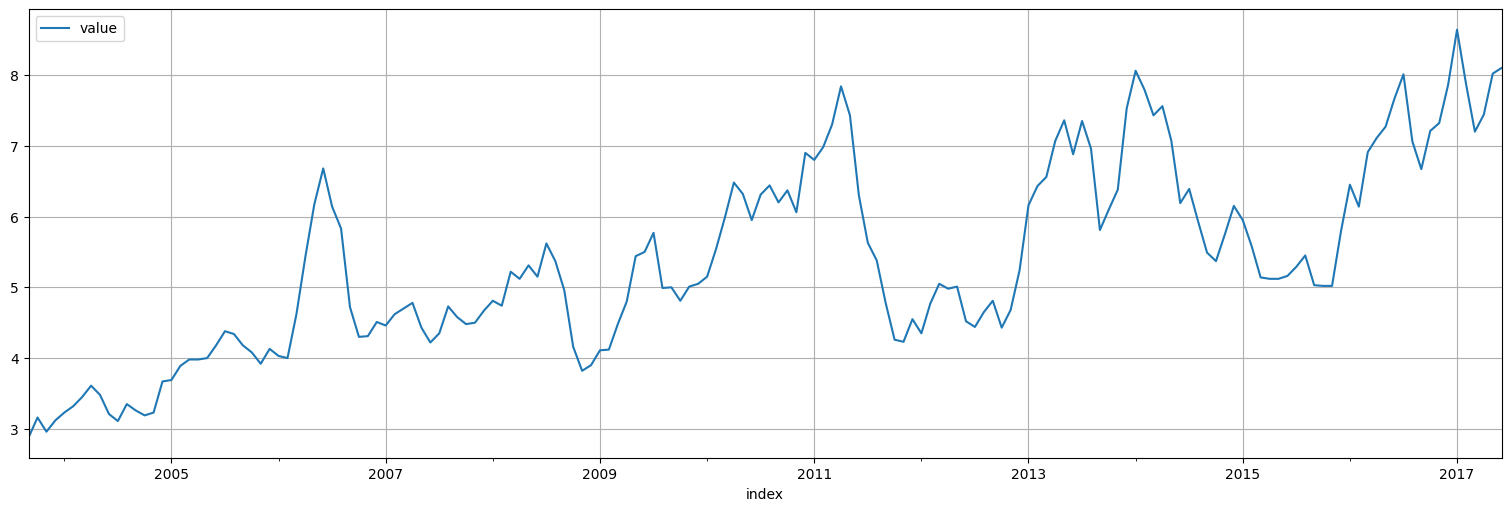
Estimación de la serie de precios de exportación del salmón noruego.¶
Considere la serie
salmonde precios de exportación de salmon noruego en dólares por kilogramo, incluida en la bibliotecaastsadel curso.Analice la autocorrelación y autocorrelación parcial de la serie.
Proponga un modelo autorregresivo de orden adecuado y ajuste el mismo. Analice los residuos obtenidos y el ajuste del modelo.
Se propone ahora un segundo modelo de la forma: $\(x_t = \beta_0 + \beta_1 t + v_t\)$
con \(v_t\) autorregresivo. Realice un ajuste por modelo lineal para estimar \(\beta_0\) y \(\beta_1\).
Con los residuos del ajuste anterior (\(v_t\)), ajuste un modelo autorregresivo de orden adecuado y compare los resultados con el modelo de la primera parte.
salmon = astsa.salmon
salmon.plot();