Análisis espectral: periodograma, regresión con componentes.¶
Componentes estacionales y periodograma¶
Otra de las componentes que nos gustaría analizar cuando exploramos un ajuste de serie temporal es la presencia de componentes periódicas.
Ejemplos:
La mezcla de \(\sin\) y \(\cos\) del ejercicio ya visto.
La serie SOI ya analizada (y también el recruitement si le creemos al libro).
Idea: ¿Como sistematizar el encontrar componentes periódicas?
Ejemplo: señal artificial (mezcla de \(\sin\) y \(\cos\))¶
import numpy as np
t=np.arange(0,500)
f=1/50 #frecuencia fundamental
signal = 0.5*np.cos(2*np.pi*f*t) + 0.5*np.sin(2*np.pi*f*t) + 0.5*np.cos(2*np.pi*2*f*t)
noise = np.random.normal(size=t.size,loc=0,scale=0.2)
x = signal + noise
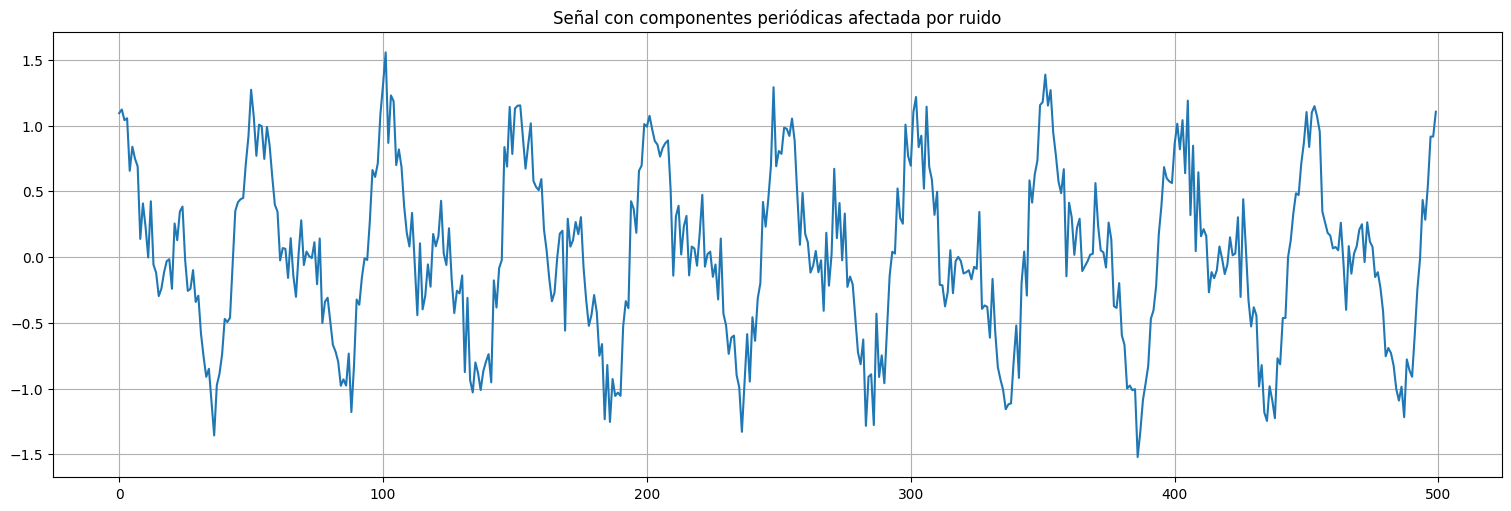
plt.plot(t,x);
plt.title("Señal con componentes periódicas afectada por ruido");
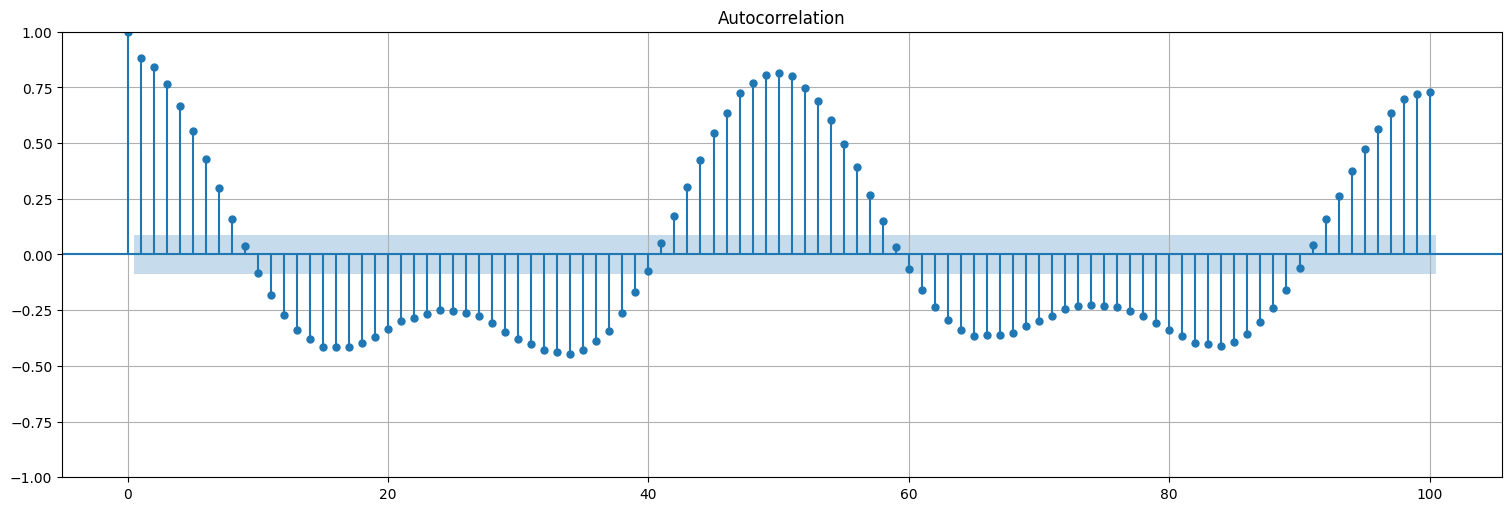
Idea 1: recurrir a la ACF¶
Calcular la autocorrelación de la señal y ver si aparecen picos. Similar a lo hecho antes para el SOI.
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(x, lags=100, bartlett_confint=False);
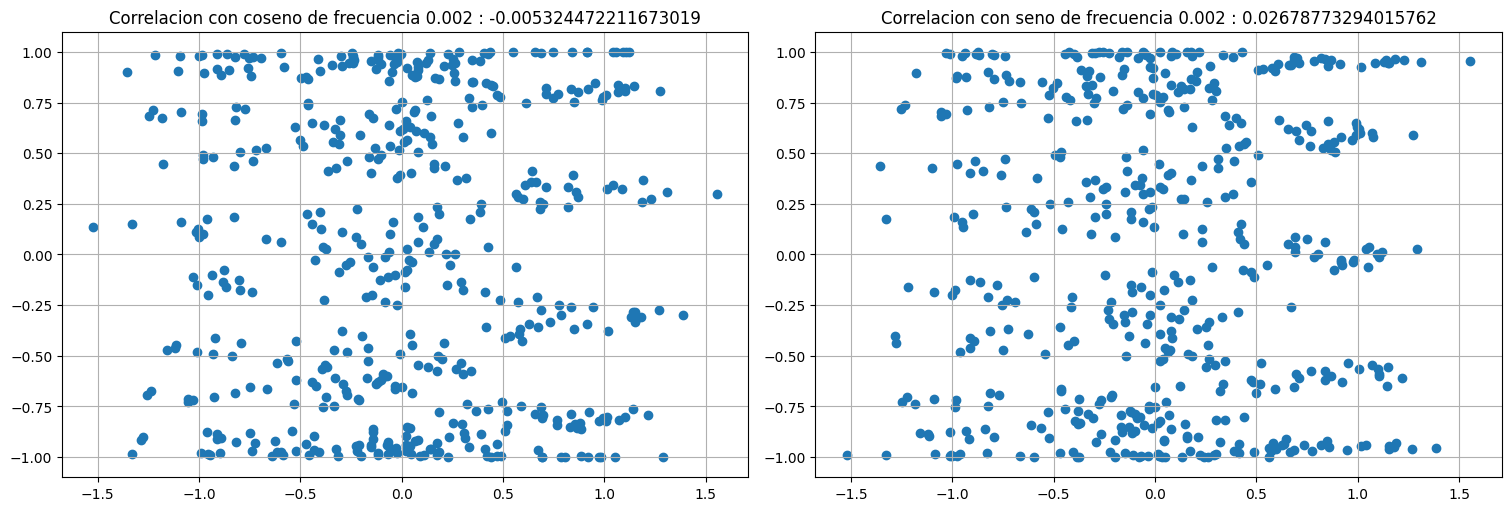
Idea 2: correlacionar con una señal de frecuencia conocida¶
La idea es tomar señales de la forma:
Si el valor \(P^f = \rho(x,c^f_t) ^2 + \rho(x,s^f_t)^2\) es alto, entonces esa frecuencia está presente en la señal. Aqui \(\rho\) indica correlación cruzada entre la señal y el \(\cos/\sin\).
Ejemplo:
#Probar con diferentes frecuencias:
f=1/500 # frecuencia a correlacionar. Si no está presente, no hay correlación.
#f=1/50 # frecuencia a correlacionar. Si está presente, hay correlación.
#f=1/25 # frecuencia a correlacionar. Si está presente, no hay correlación.
c1 = np.cos(2*np.pi*f*t)
s1 = np.sin(2*np.pi*f*t)
plt.subplot(1, 2,1)
plt.scatter(x,c1)
plt.title(f"Correlacion con coseno de frecuencia {f} : {np.corrcoef(x,c1)[0,1]}");
plt.subplot(1,2,2)
plt.scatter(x,s1)
plt.title(f"Correlacion con seno de frecuencia {f} : {np.corrcoef(x,s1)[0,1]}");
Periodograma (transformada discreta de Fourier)¶
El periodograma es una forma sistemática de recorrer las correlaciones anteriores y calcular cuáles son significativas.
Definición: Transformada Discreta de Fourier
Dada una serie temporal \(x_t\) de largo \(n\) se define su DFT (Discrete Fourier Transform) como el vector complejo:
\[DFT_x(j/n) = \sum_{t} x_t \cos\left(2\pi \frac{j}{n} t\right) - i \sum_{t} x_t \sin\left(2\pi \frac{j}{n} t\right) = \rho(x,c^{j/n}_t) - i \rho(x,s^{j/n}_t)\]
Si \(x_t\) está centrada, \(DFT_x\) guarda las covarianzas (correlaciones no escaladas) con cosenos y senos de las frecuencias de la forma \(j/n\) siendo \(n\) la cantidad de datos.
Observar que el módulo \(|DFT_x(j/n)|^2 = \rho(x,c^{j/n}_t) ^2 + \rho(x,s^{j/n}_t)^2\) nos da idea de la “fuerza” de esta frecuencia.
El rol de \(j\)¶
La idea de la DFT es calcular sistemáticamente las correlaciones contra las frecuencias de la forma \(j/n\), siendo \(n\) el largo de los datos.
\(j=0\) correspondería a \(\cos(0) \equiv 1\) y \(\sin(0)\equiv 0\), que es lo mismo que sumar los datos. Es por ello que conviene centrar los datos antes de trabajar (eliminar la media).
\(0<j<n/2\) corresponde a las frecuencias observables. La interpretación de \(j\) aquí es la cantidad de ciclos en la muestra que se presentan a dicha frecuencia.
Ejemplo: En una serie de frecuencia anual (\(12\) muestras por año) y \(120\) observaciones (\(10\) años), una componente anual debería aparecer para \(j=10\) (\(10\) ciclos en la muestra) o bien \(j/n=10/120=1/12\).
\(j=n/2\) es la máxima frecuencia observable. ¿Por qué? Porque para poder “observar” adecuadamente una frecuencia necesitamos al menos dos muestras por ciclo. Si tenemos \(n\) datos, dicha frecuencia máxima corresponde a \(j=n/2\) ciclos en la muestra.
FFT: Fast Fourier Transform¶
Numéricamente se calcula la \(DFT\) usando el algoritmo FFT: Fast Fourier Transform, que reusa varios de los cálculos de correlación para una implementación más eficiente.
En python usando numpy:
La FFT (DFT) se obtiene mediante
numpy.fft(x).Se calcula \(I(j/n) = |DFT_x (j/n)|^2\), el módulo cuadrado del complejo resultante.
Luego se obtiene el Periodograma \(P\) escalado definido como: $\(P(j/n) = \frac{4}{n^2} I(j/n) , \quad j=0,\ldots,n/2.\)\( El coeficiente \)4/n^2$ lleva la escala a los coeficientes de regresión contra seno y coseno.
Si se desea graficar el periodograma \(P\) en las frecuencias originales de la serie, se debe usar en las abscisas el vector de frecuencias:
f = [0, 1/n, 2/n, ..., (n/2-1)/n] * freqsiendo
freqla frecuencia de la serie (frecuencia de muestreo).
Utilizando este método definimos la siguiente función que calcula el periodograma escalado para una serie:
def periodogram(x,sampling_frequency=1):
"""Función que calcula el periodograma y grafica.
Parameters
----------
x : array_like, data.
sampling_frequency: frecuencia de muestreo de la serie, para graficar.
"""
n = x.size
P = 4/n**2 * np.abs(np.fft.fft(x))**2
P = P[0:round(n/2)]
f = np.arange(0,round(n/2))/n * sampling_frequency
plt.stem(f,P,basefmt='');
plt.xlabel("Frequency")
plt.ylabel("Power")
periodogram(x)
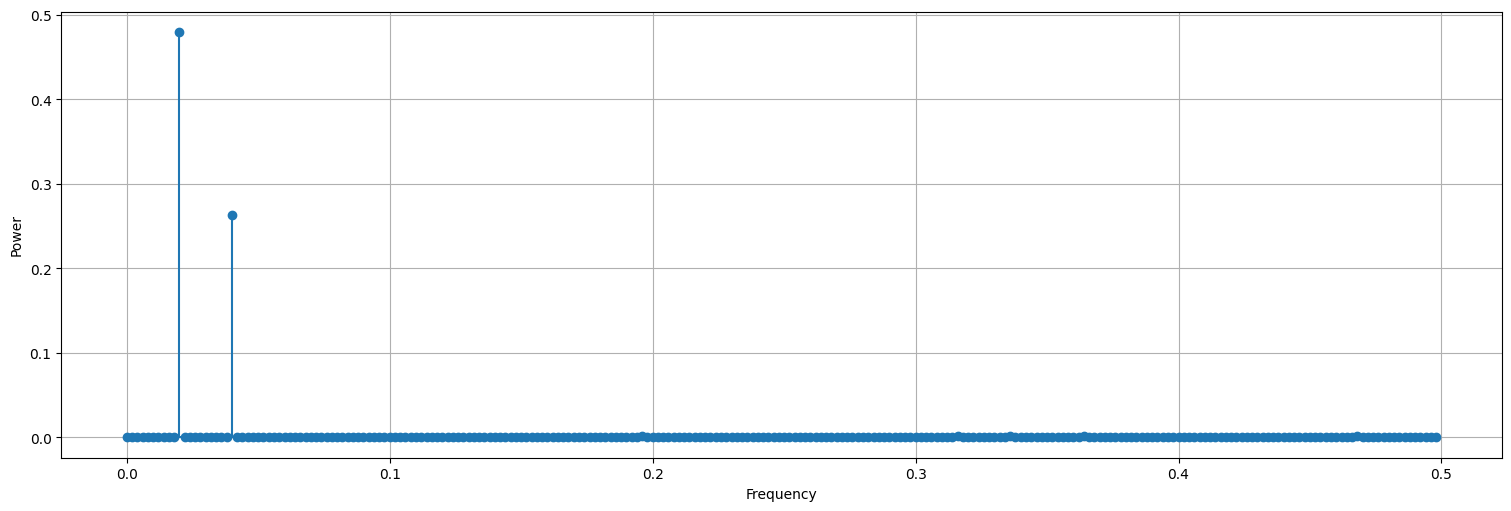
Observación¶
Notar que las alturas del periodograma guardan relación con los coeficientes de seno y coseno involucrados en la señal.
Análisis espectral¶
Con la misma idea podemos hacer una función que indique cuáles fueron las frecuencias más importantes:
import pandas as pd
def spectrum(x,sampling_frequency=1, nfreq=10):
"""Función que calcula las componentes más relevantes del periodograma.
Parameters
----------
x : array_like, data.
sampling_frequency: frecuencia de muestreo de la serie, para graficar.
"""
n = x.size
nfreq = np.minimum(nfreq,round(n/2)) #corto nfreq si la serie es muy corta!
P = 4/n**2 * np.abs(np.fft.fft(x))**2
P = P[0:round(n/2)]
f = np.arange(0,round(n/2))/n * sampling_frequency
index = np.argsort(P)[::-1] #ordeno P decreciente
return pd.DataFrame({"Frecuencia" : f[index[0:nfreq]],"Potencia" : P[index[0:nfreq]]})
df = spectrum(x)
print(df)
Frecuencia Potencia
0 0.020 0.479893
1 0.040 0.263745
2 0.196 0.001549
3 0.336 0.001422
4 0.468 0.001235
5 0.316 0.001145
6 0.364 0.001123
7 0.288 0.001105
8 0.066 0.001056
9 0.000 0.001028
Regresión lineal para ajustar¶
Luego de identificadas las frecuencias más relevantes, el último paso es simplemente ajustar una regresión lineal incluyendo todos los términos que sean necesarios.
Ejemplo:¶
En el caso anterior identificamos las frecuencias \(0.02\) y \(0.04\) que estaban en la serie original. Hacemos entonces una regresión de la forma:
y luego analizamos los residuos. Si sabemos que la serie está centrada podemos prescindir de \(\beta_0\) (el intercept).
from statsmodels.formula.api import ols
t = np.arange(0,500)
data = pd.Series({"x":x,"time":t})
fit = ols(formula='x~np.cos(2*np.pi*0.02*time) + np.sin(2*np.pi*0.02*time) + np.cos(2*np.pi*0.04*time) + np.sin(2*np.pi*0.04*time)', data=data).fit()
fit.summary()
| Dep. Variable: | x | R-squared: | 0.908 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.907 |
| Method: | Least Squares | F-statistic: | 1216. |
| Date: | Tue, 22 Apr 2025 | Prob (F-statistic): | 2.02e-254 |
| Time: | 16:13:58 | Log-Likelihood: | 109.17 |
| No. Observations: | 500 | AIC: | -208.3 |
| Df Residuals: | 495 | BIC: | -187.3 |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.0160 | 0.009 | 1.834 | 0.067 | -0.001 | 0.033 |
| np.cos(2 * np.pi * 0.02 * time) | 0.4928 | 0.012 | 39.856 | 0.000 | 0.468 | 0.517 |
| np.sin(2 * np.pi * 0.02 * time) | 0.4869 | 0.012 | 39.381 | 0.000 | 0.463 | 0.511 |
| np.cos(2 * np.pi * 0.04 * time) | 0.5135 | 0.012 | 41.533 | 0.000 | 0.489 | 0.538 |
| np.sin(2 * np.pi * 0.04 * time) | -0.0074 | 0.012 | -0.599 | 0.550 | -0.032 | 0.017 |
| Omnibus: | 0.735 | Durbin-Watson: | 2.071 |
|---|---|---|---|
| Prob(Omnibus): | 0.692 | Jarque-Bera (JB): | 0.750 |
| Skew: | 0.093 | Prob(JB): | 0.687 |
| Kurtosis: | 2.960 | Cond. No. | 1.41 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Luego descartamos los no significativos (ej: el intercept y el seno de frecuencia alta en este caso).
fit = ols(formula='x~0+np.cos(2*np.pi*0.02*time) + np.sin(2*np.pi*0.02*time) + np.cos(2*np.pi*0.04*time)', data=data).fit()
fit.summary()
| Dep. Variable: | x | R-squared (uncentered): | 0.907 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.906 |
| Method: | Least Squares | F-statistic: | 1616. |
| Date: | Tue, 22 Apr 2025 | Prob (F-statistic): | 7.73e-256 |
| Time: | 16:13:58 | Log-Likelihood: | 107.30 |
| No. Observations: | 500 | AIC: | -208.6 |
| Df Residuals: | 497 | BIC: | -195.9 |
| Df Model: | 3 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| np.cos(2 * np.pi * 0.02 * time) | 0.4928 | 0.012 | 39.787 | 0.000 | 0.468 | 0.517 |
| np.sin(2 * np.pi * 0.02 * time) | 0.4869 | 0.012 | 39.313 | 0.000 | 0.463 | 0.511 |
| np.cos(2 * np.pi * 0.04 * time) | 0.5135 | 0.012 | 41.461 | 0.000 | 0.489 | 0.538 |
| Omnibus: | 0.696 | Durbin-Watson: | 2.055 |
|---|---|---|---|
| Prob(Omnibus): | 0.706 | Jarque-Bera (JB): | 0.710 |
| Skew: | 0.090 | Prob(JB): | 0.701 |
| Kurtosis: | 2.961 | Cond. No. | 1.00 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Ajuste:¶
plt.plot(t,x, label="Observaciones");
plt.plot(t,fit.fittedvalues, label="Ajuste");
plt.legend();
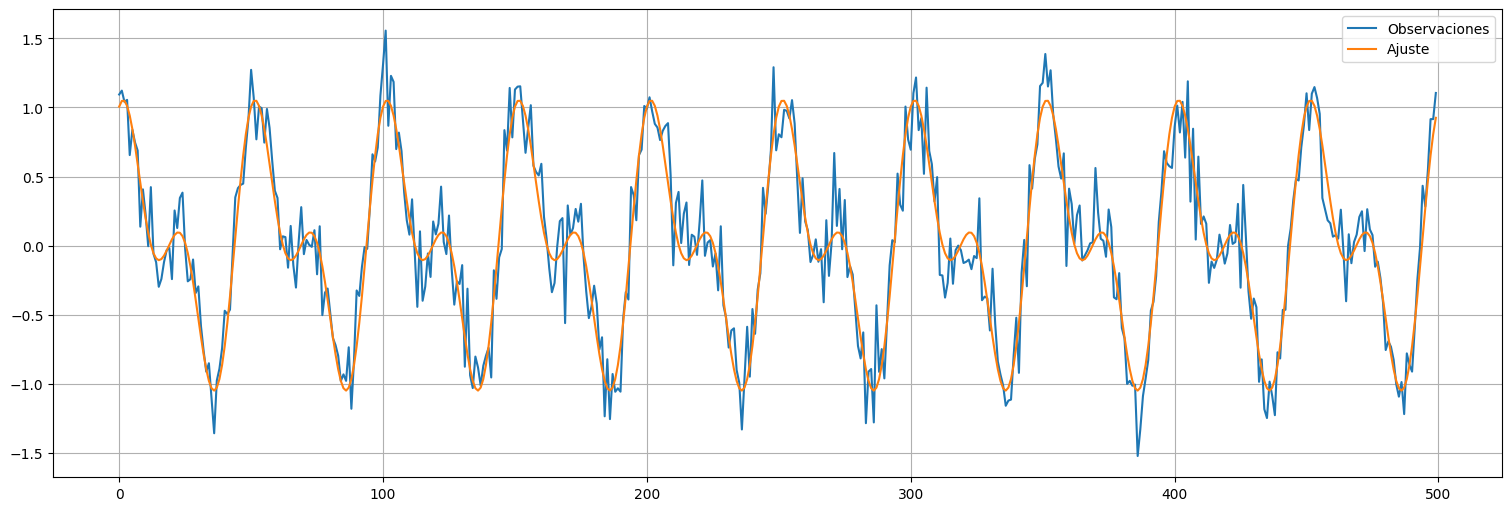
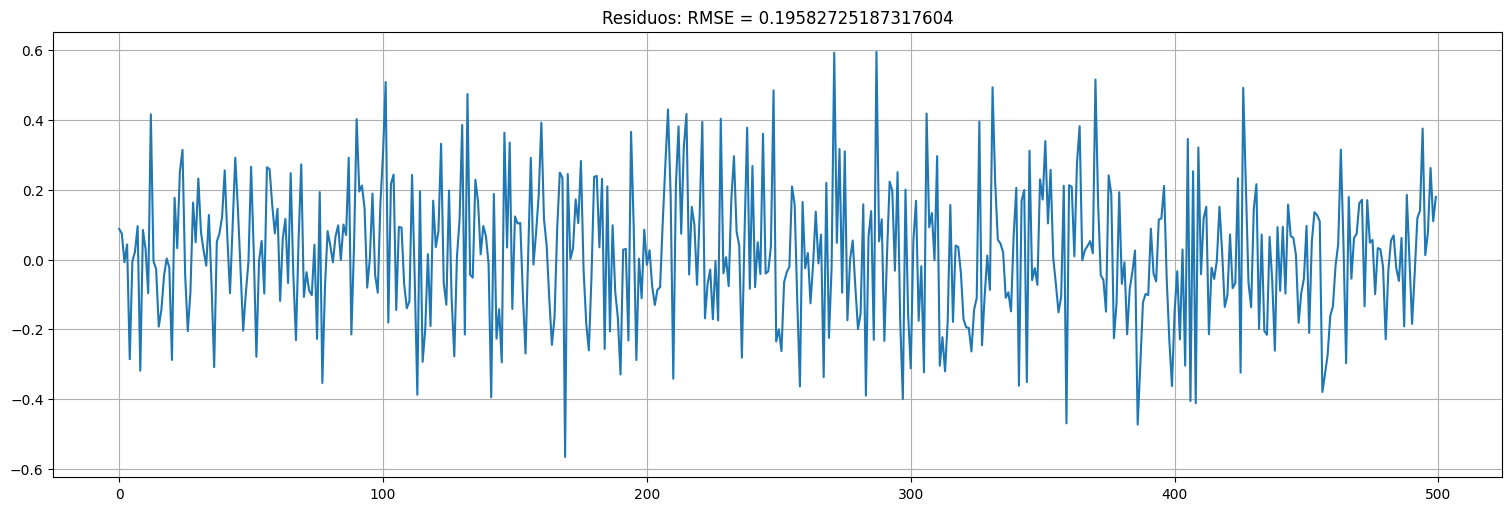
Residuos:¶
plt.plot(t,fit.resid);
plt.title(f"Residuos: RMSE = {np.sqrt(fit.mse_resid)}");
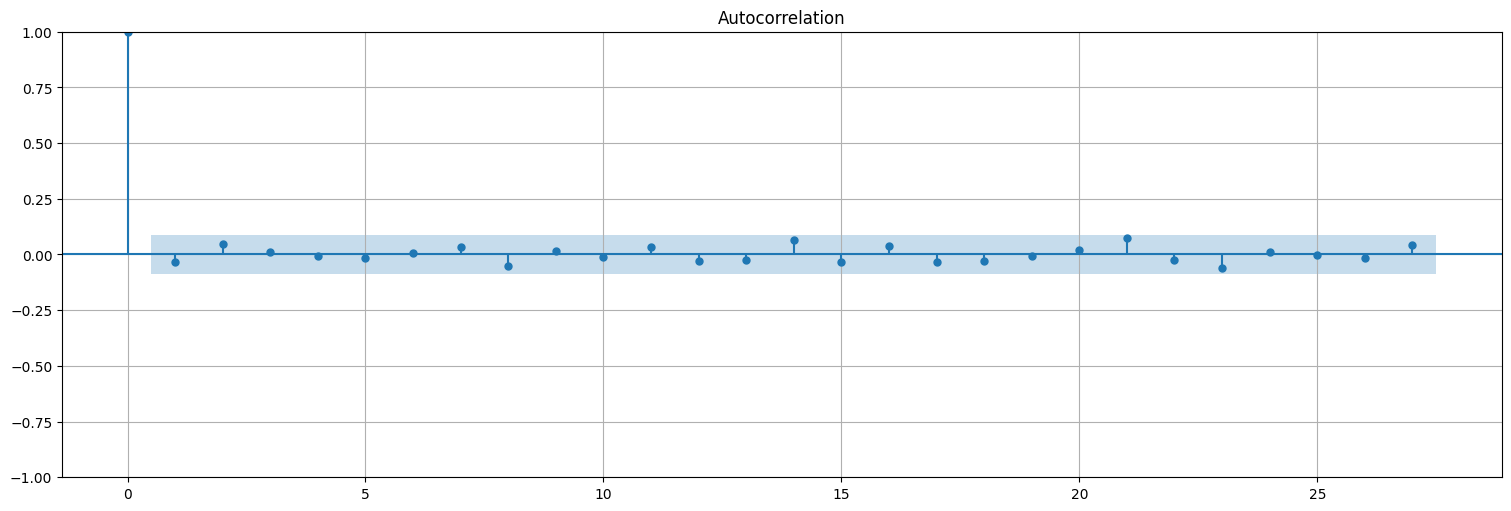
plot_acf(fit.resid,bartlett_confint=False);
Aplicación:¶
Apliquemos la idea del periodograma a las series SOI y Recruitement de la biblioteca astsa
soi = astsa.soi
rec = astsa.rec
soi.head() #notar que las medidas son mensuales
| value | |
|---|---|
| index | |
| 1950-01 | 0.377 |
| 1950-02 | 0.246 |
| 1950-03 | 0.311 |
| 1950-04 | 0.104 |
| 1950-05 | -0.016 |
Importante:¶
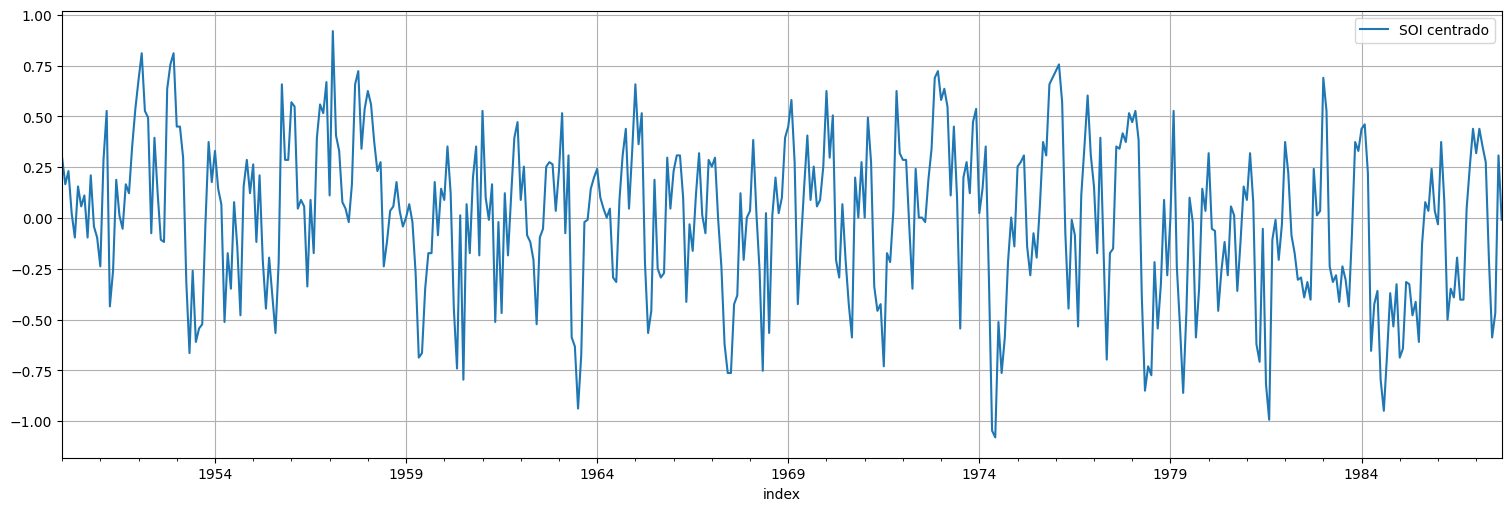
Como ya mencionamos, antes de calcular el periodograma, debemos centrar la serie.
s = soi-np.mean(soi)
s.plot().legend(["SOI centrado"]);
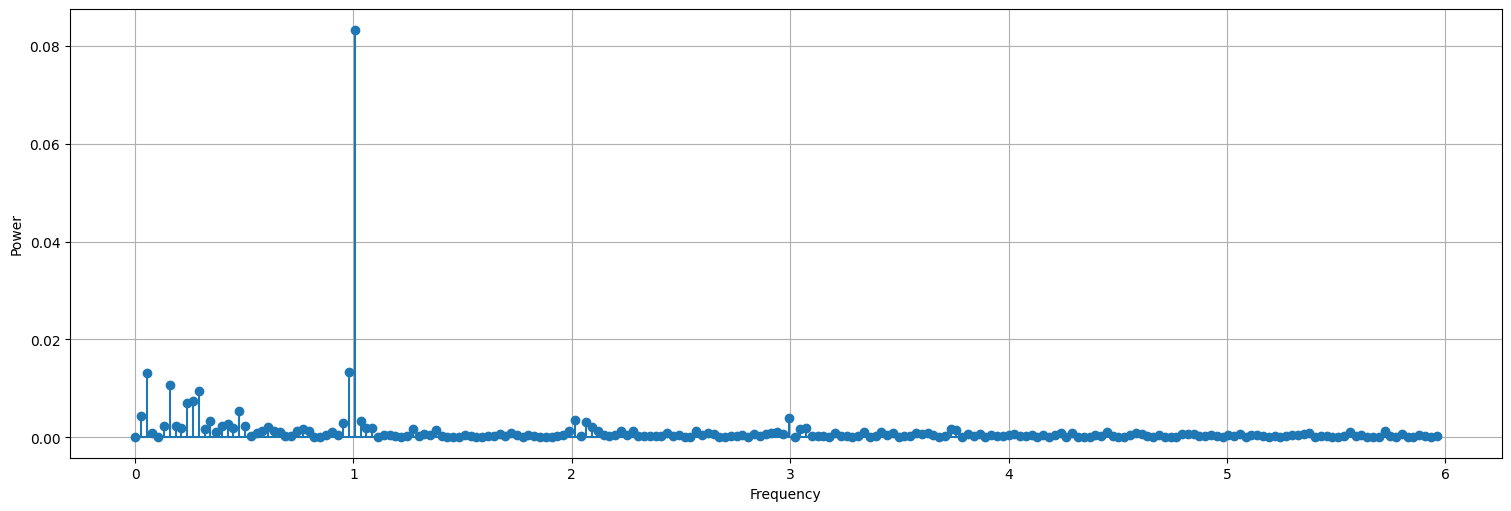
periodogram(s.value, sampling_frequency=12)
spectrum(s.value, sampling_frequency=12)
| Frecuencia | Potencia | |
|---|---|---|
| 0 | 1.006623 | 0.083315 |
| 1 | 0.980132 | 0.013316 |
| 2 | 0.052980 | 0.013200 |
| 3 | 0.158940 | 0.010678 |
| 4 | 0.291391 | 0.009385 |
| 5 | 0.264901 | 0.007391 |
| 6 | 0.238411 | 0.006961 |
| 7 | 0.476821 | 0.005480 |
| 8 | 0.026490 | 0.004373 |
| 9 | 2.993377 | 0.004042 |
Luego hacemos la regresión, volviendo a incorporar el intercept con los datos sin centrar. El intercept se hace cargo de la media.
time = pd.Series(np.arange(0,soi.size)/12,index=soi.index) #creo una columna de tiempos
data = pd.concat([time,soi], axis=1)
data.columns = ["time","soi"]
fit = ols(formula="soi~np.cos(2*np.pi*time) + np.sin(2*np.pi*time)",data=data).fit()
fit.summary()
| Dep. Variable: | soi | R-squared: | 0.355 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.352 |
| Method: | Least Squares | F-statistic: | 123.8 |
| Date: | Tue, 22 Apr 2025 | Prob (F-statistic): | 1.47e-43 |
| Time: | 16:13:59 | Log-Likelihood: | -107.94 |
| No. Observations: | 453 | AIC: | 221.9 |
| Df Residuals: | 450 | BIC: | 234.2 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.0815 | 0.014 | 5.627 | 0.000 | 0.053 | 0.110 |
| np.cos(2 * np.pi * time) | 0.3082 | 0.020 | 15.073 | 0.000 | 0.268 | 0.348 |
| np.sin(2 * np.pi * time) | -0.0937 | 0.020 | -4.571 | 0.000 | -0.134 | -0.053 |
| Omnibus: | 5.111 | Durbin-Watson: | 1.078 |
|---|---|---|---|
| Prob(Omnibus): | 0.078 | Jarque-Bera (JB): | 4.859 |
| Skew: | -0.206 | Prob(JB): | 0.0881 |
| Kurtosis: | 2.705 | Cond. No. | 1.42 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
plt.plot(time,soi, label="Observaciones");
plt.plot(time,fit.fittedvalues, label="Ajuste");
plt.legend();
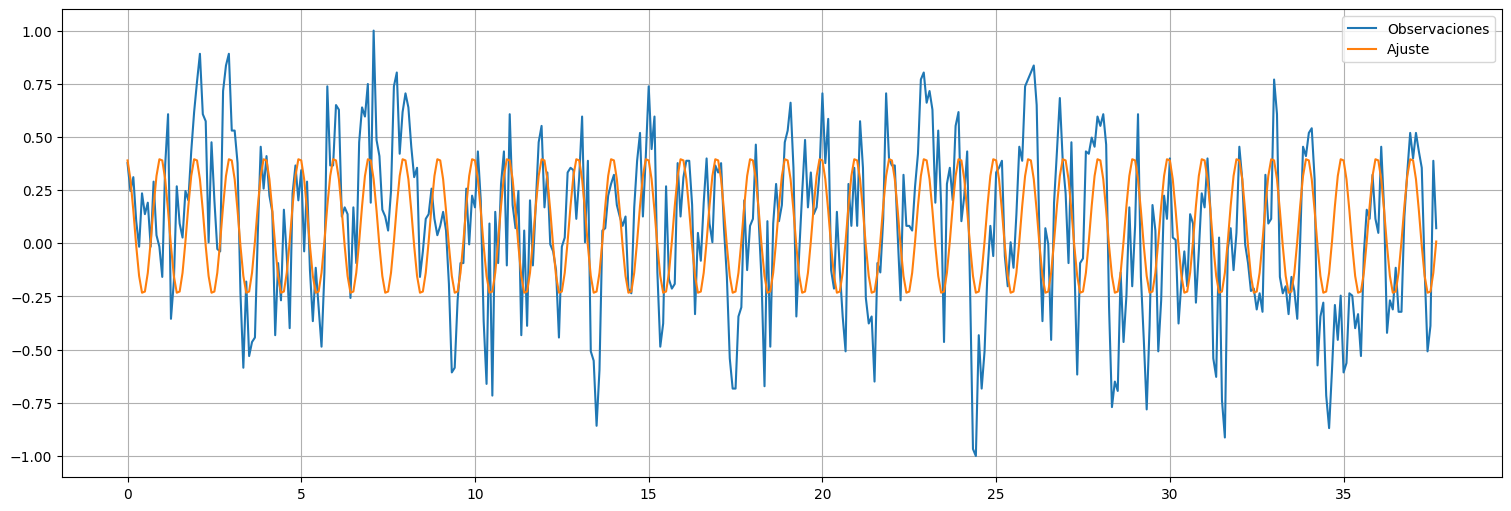
Agregamos ahora componentes de baja frecuencia del espectro:
f0 = 1.0
f1 = 0.052980
f2 = 0.158940
fit = ols(formula="soi~np.cos(2*np.pi*f0*time) + np.sin(2*np.pi*f0*time) + np.cos(2*np.pi*f1*time) + np.sin(2*np.pi*f1*time) + np.cos(2*np.pi*f2*time) + np.sin(2*np.pi*f2*time) ",data=data).fit()
fit.summary()
| Dep. Variable: | soi | R-squared: | 0.438 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.430 |
| Method: | Least Squares | F-statistic: | 57.83 |
| Date: | Tue, 22 Apr 2025 | Prob (F-statistic): | 8.95e-53 |
| Time: | 16:13:59 | Log-Likelihood: | -76.873 |
| No. Observations: | 453 | AIC: | 167.7 |
| Df Residuals: | 446 | BIC: | 196.6 |
| Df Model: | 6 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.0815 | 0.014 | 6.000 | 0.000 | 0.055 | 0.108 |
| np.cos(2 * np.pi * f0 * time) | 0.3087 | 0.019 | 16.093 | 0.000 | 0.271 | 0.346 |
| np.sin(2 * np.pi * f0 * time) | -0.0939 | 0.019 | -4.885 | 0.000 | -0.132 | -0.056 |
| np.cos(2 * np.pi * f1 * time) | 0.0057 | 0.019 | 0.295 | 0.768 | -0.032 | 0.043 |
| np.sin(2 * np.pi * f1 * time) | 0.1150 | 0.019 | 5.987 | 0.000 | 0.077 | 0.153 |
| np.cos(2 * np.pi * f2 * time) | 0.0338 | 0.019 | 1.759 | 0.079 | -0.004 | 0.072 |
| np.sin(2 * np.pi * f2 * time) | 0.0989 | 0.019 | 5.152 | 0.000 | 0.061 | 0.137 |
| Omnibus: | 7.674 | Durbin-Watson: | 1.236 |
|---|---|---|---|
| Prob(Omnibus): | 0.022 | Jarque-Bera (JB): | 7.513 |
| Skew: | -0.280 | Prob(JB): | 0.0234 |
| Kurtosis: | 2.710 | Cond. No. | 1.43 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
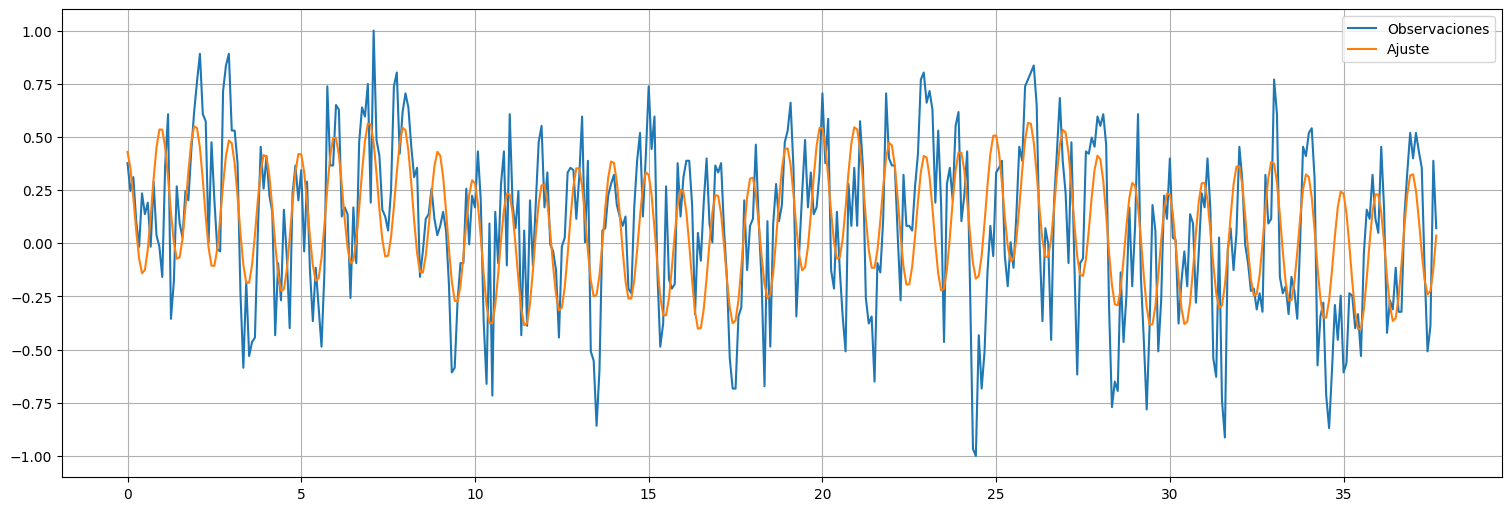
plt.plot(time,soi, label="Observaciones");
plt.plot(time,fit.fittedvalues, label="Ajuste");
plt.legend();
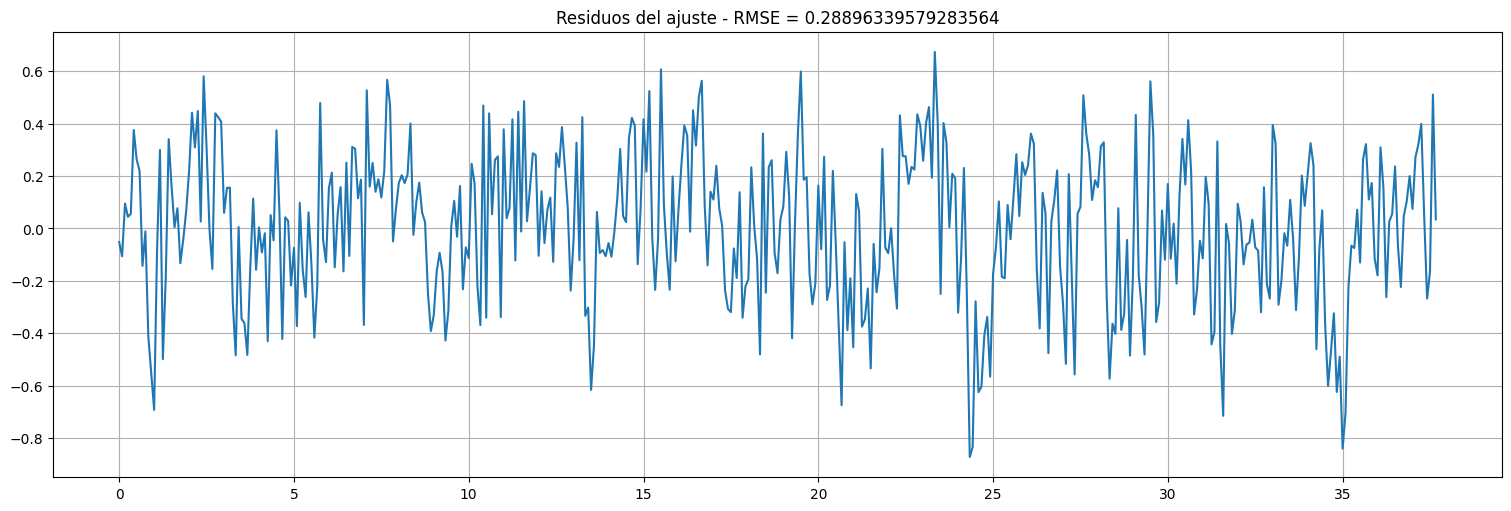
plt.plot(time,fit.resid);
plt.title(f"Residuos del ajuste - RMSE = {np.sqrt(fit.mse_resid)}");
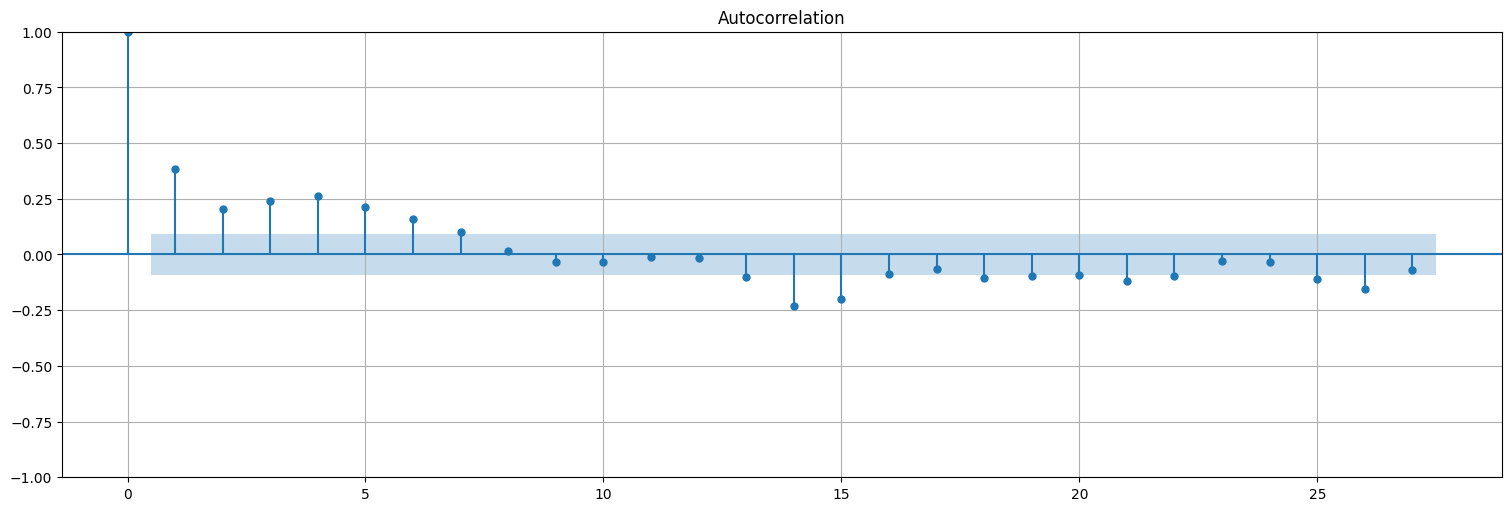
plot_acf(fit.resid, bartlett_confint=False);
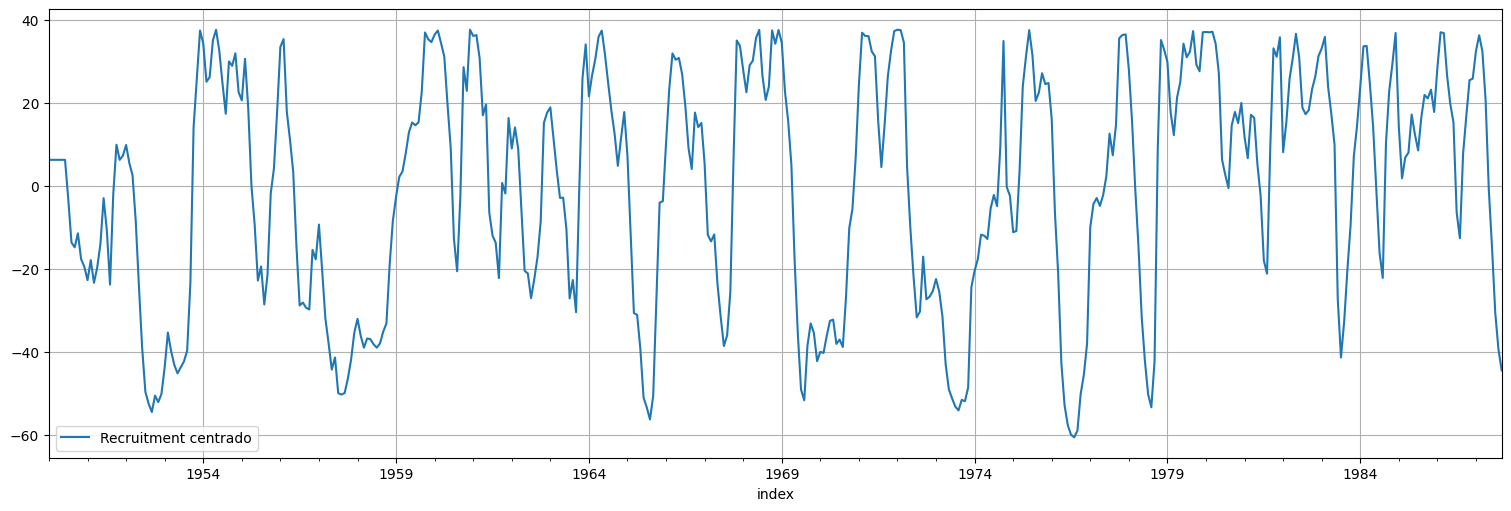
Podemos hacer lo mismo para el Recruitment…
r = rec - np.mean(rec)
r.plot().legend(["Recruitment centrado"]);
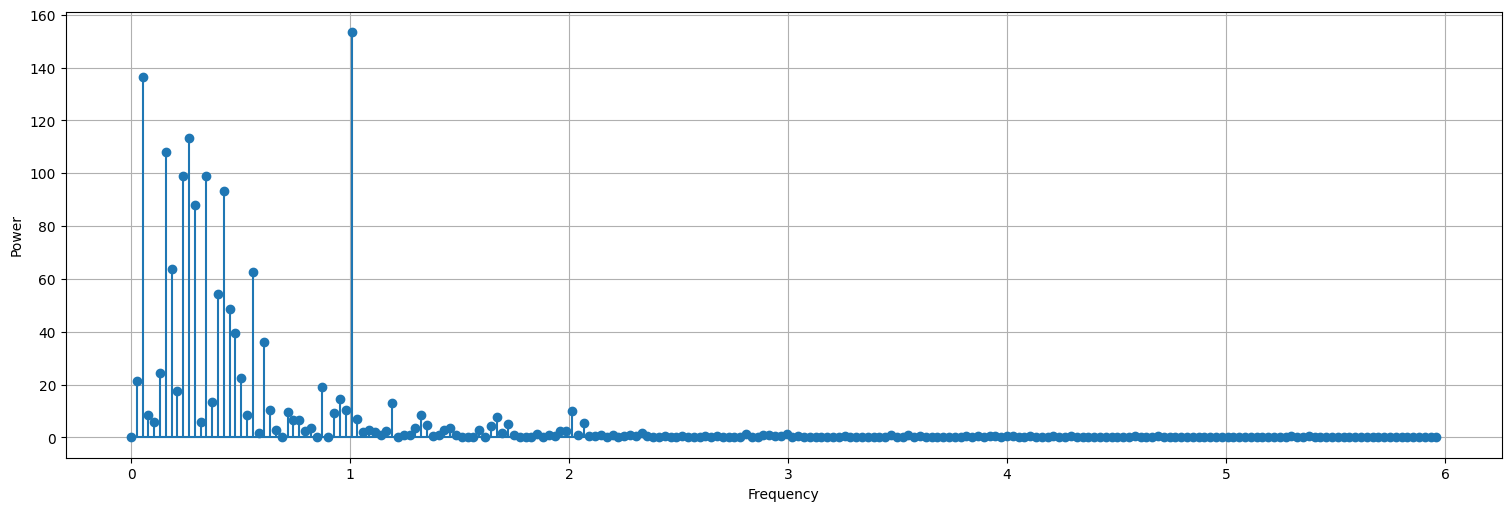
periodogram(r.value, sampling_frequency=12)
Observaciones¶
La frecuencia anual aparece en el periodograma (el pico es en \(j=38\), cuando la muestra tiene casi \(38\) años de datos precisamente). No era clara en la correlación en el caso de
recpero aquí sí se observa claramente.Aparecen frecuencias más lentas, tanto en
soicomo enrec. En el caso derecaparecen varios picos en frecuencias casi contiguas, de períodos mayores a un año.No siempre los picos son todos relevantes. A veces es necesario suavizar el periodograma para extraer las frecuencias relevantes.
Por ejemplo, aparecen picos cercanos a \(f=0.25\) que corresponden con el ciclo el fenómeno del Niño (cada 4 años).
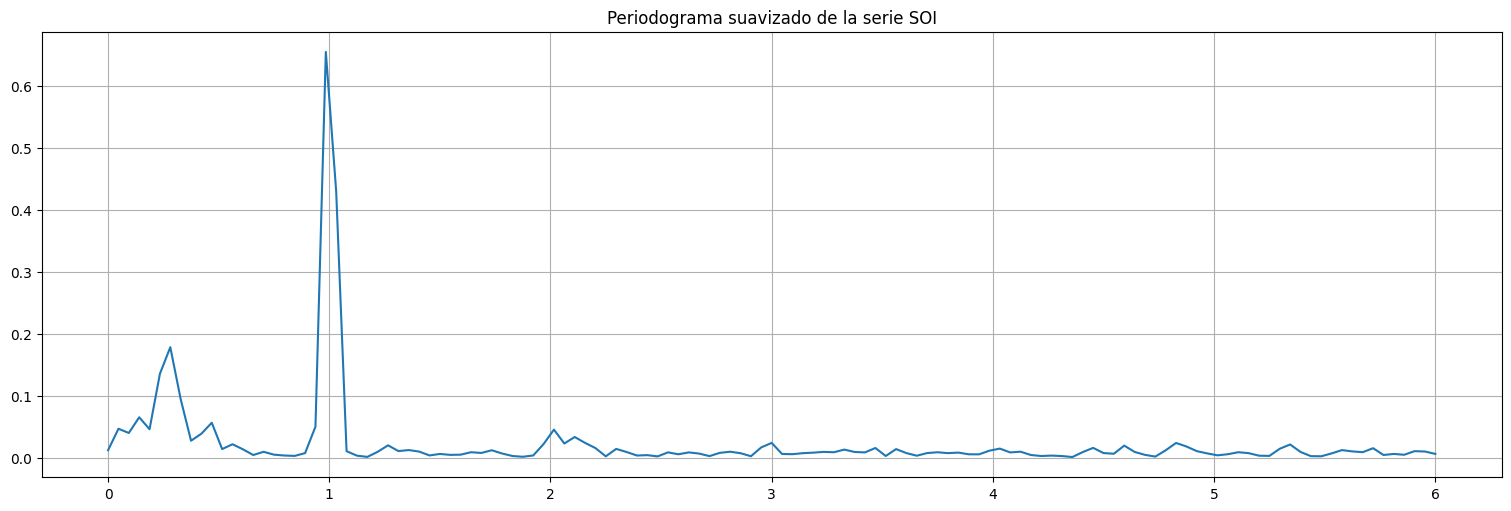
Periodograma de Welch¶
Una forma de suavizar el periodograma anterior es realizar la transformación en ventanas más cortas de la serie, analizar la \(DFT\) en cada ventana y promediar. Este método se denomina periodograma de Welch.
from scipy.signal import welch
f,P = welch(soi.value.values,fs=12)
plt.plot(f,P)
plt.title("Periodograma suavizado de la serie SOI");
from scipy.signal import welch
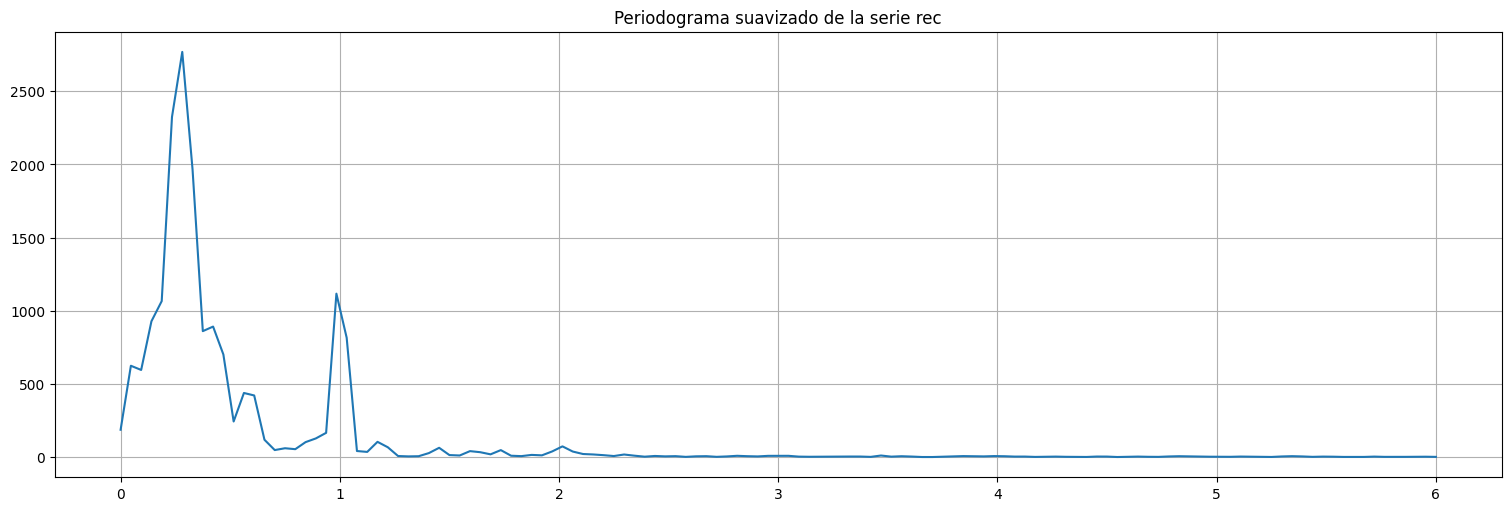
f,P = welch(rec.value.values,fs=12)
plt.plot(f,P)
plt.title("Periodograma suavizado de la serie rec");
Un ejemplo completo: la serie Air Passengers¶
Esta es una serie clásica que también analizaremos con otras técnicas más adelante. Por ahora veamos como podemos combinar todo lo visto anteriormente para hacer un ajuste.
Se tiene \(x_t=\) miles de pasajeros mensuales internacionales en el transporte aéreo.
df = pd.read_csv('../data/international-airline-passengers.csv', names = ['year','passengers'], header=0)
air = pd.Series(df["passengers"].values, index=np.arange(1949,1961,1/12))
time = pd.Series(np.arange(1949,1961,1/12), index=np.arange(1949,1961,1/12))
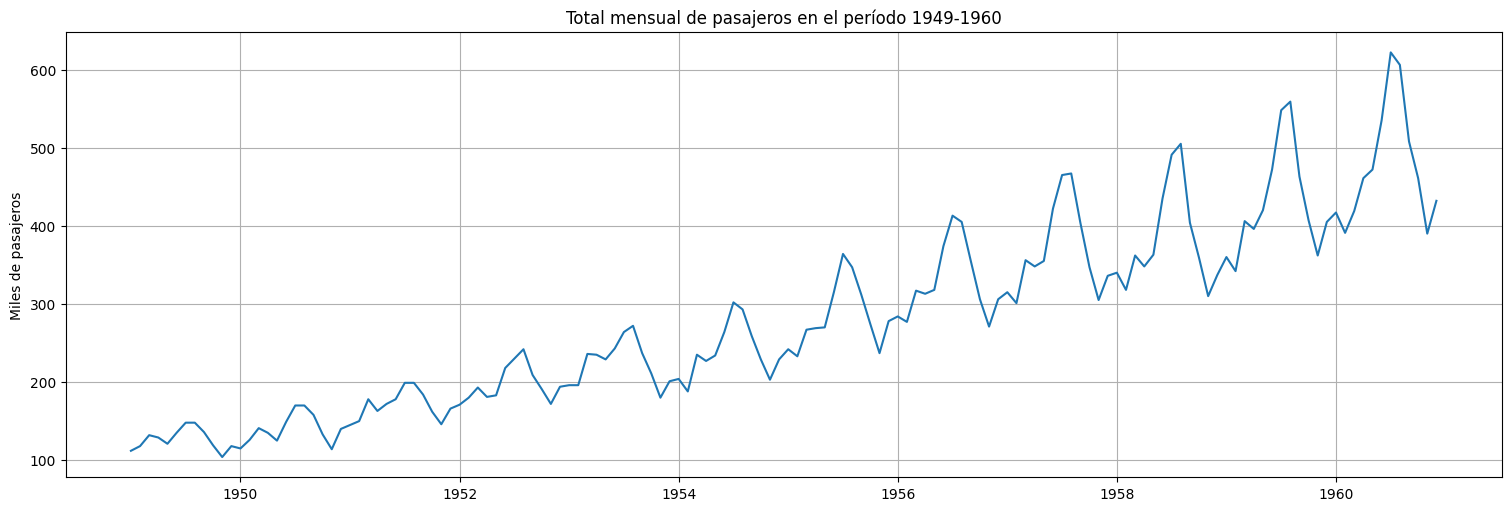
air.plot();
plt.title("Total mensual de pasajeros en el período 1949-1960")
plt.ylabel("Miles de pasajeros");
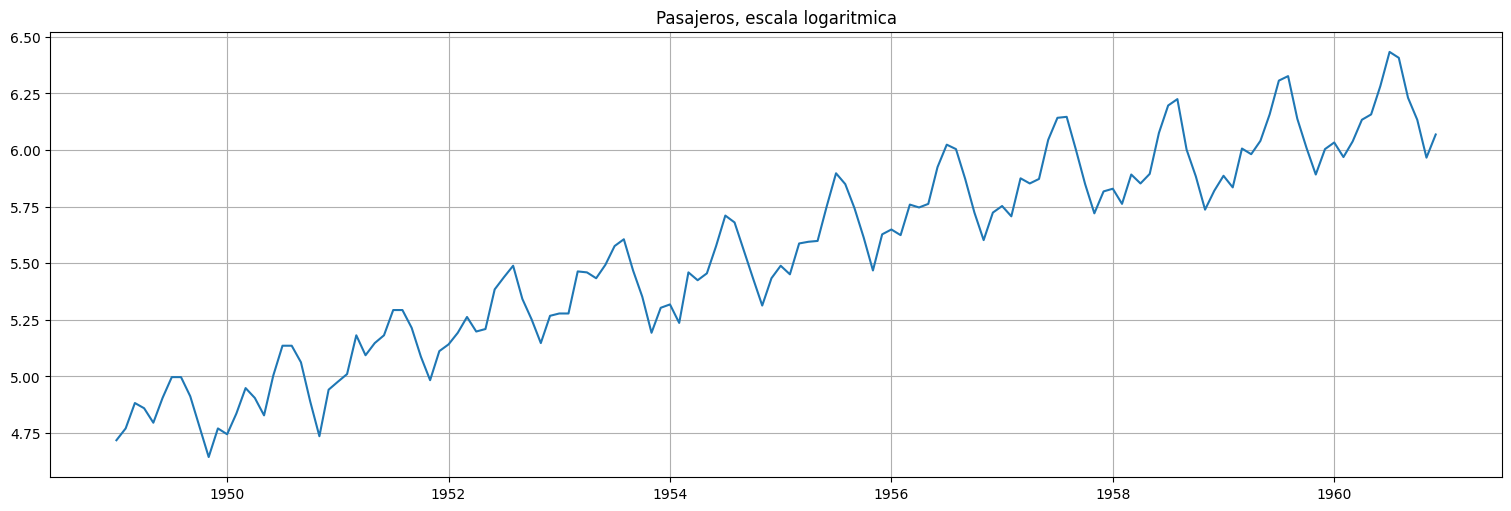
logair = np.log(air);
logair.plot();
plt.title("Pasajeros, escala logaritmica");
data = pd.concat([air,time], axis=1)
fit = ols(formula="logair~time", data=data).fit()
fit.summary()
| Dep. Variable: | logair | R-squared: | 0.902 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.901 |
| Method: | Least Squares | F-statistic: | 1300. |
| Date: | Tue, 22 Apr 2025 | Prob (F-statistic): | 2.41e-73 |
| Time: | 16:14:00 | Log-Likelihood: | 80.794 |
| No. Observations: | 144 | AIC: | -157.6 |
| Df Residuals: | 142 | BIC: | -151.6 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -230.1878 | 6.539 | -35.203 | 0.000 | -243.114 | -217.262 |
| time | 0.1206 | 0.003 | 36.050 | 0.000 | 0.114 | 0.127 |
| Omnibus: | 3.750 | Durbin-Watson: | 0.587 |
|---|---|---|---|
| Prob(Omnibus): | 0.153 | Jarque-Bera (JB): | 2.722 |
| Skew: | 0.184 | Prob(JB): | 0.256 |
| Kurtosis: | 2.436 | Cond. No. | 1.10e+06 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.1e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
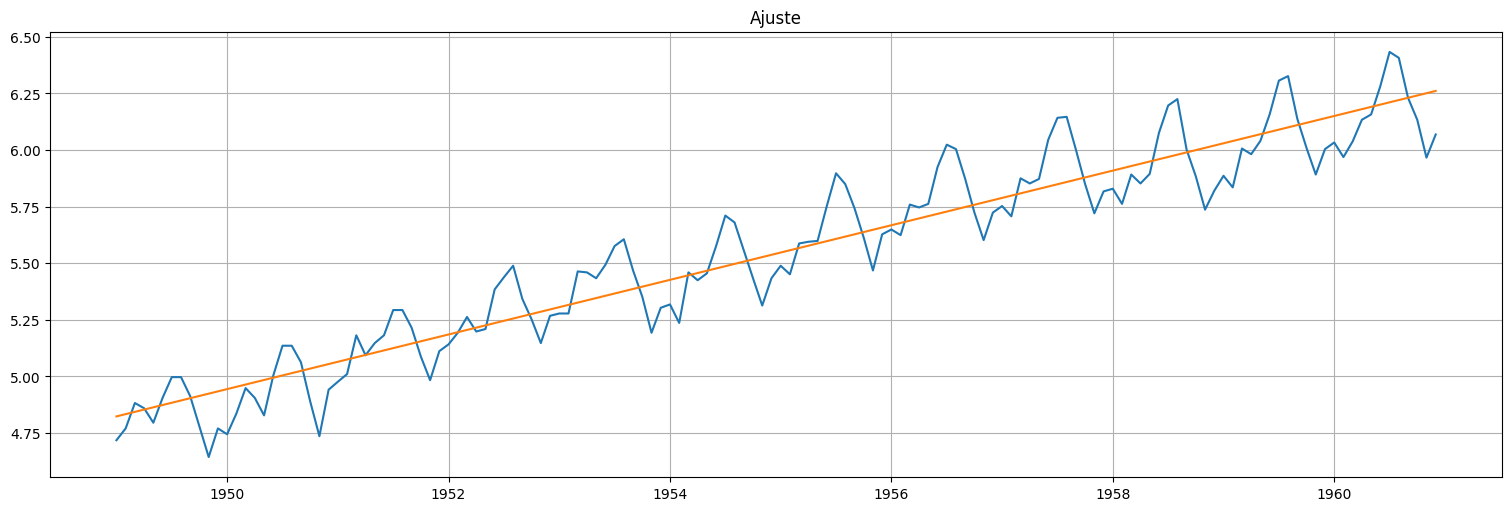
logair.plot()
fit.fittedvalues.plot();
plt.title("Ajuste");
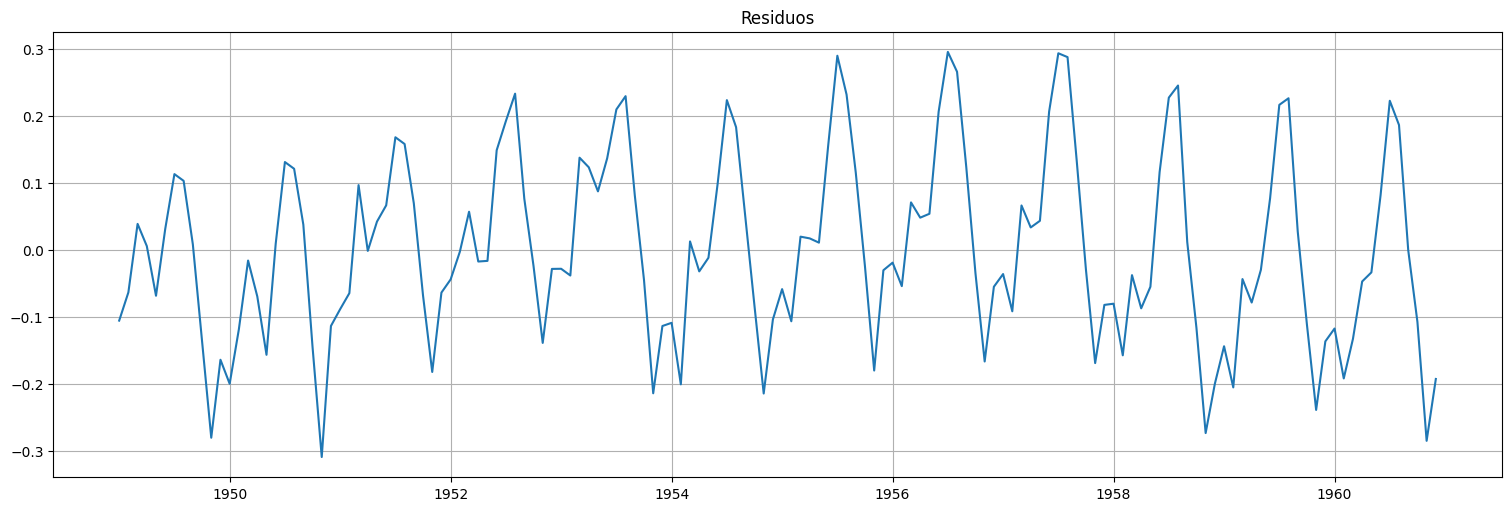
fit.resid.plot()
plt.title("Residuos");
fit = ols(formula="logair~time+np.cos(2*np.pi*time)+np.sin(2*np.pi*time)+np.cos(2*np.pi*2*time)+np.sin(2*np.pi*2*time)", data=air).fit()
fit.summary()
| Dep. Variable: | logair | R-squared: | 0.977 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.976 |
| Method: | Least Squares | F-statistic: | 1177. |
| Date: | Tue, 22 Apr 2025 | Prob (F-statistic): | 3.03e-111 |
| Time: | 16:14:01 | Log-Likelihood: | 185.79 |
| No. Observations: | 144 | AIC: | -359.6 |
| Df Residuals: | 138 | BIC: | -341.8 |
| Df Model: | 5 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -230.9817 | 3.208 | -71.998 | 0.000 | -237.325 | -224.638 |
| time | 0.1210 | 0.002 | 73.725 | 0.000 | 0.118 | 0.124 |
| np.cos(2 * np.pi * time) | -0.1475 | 0.008 | -18.392 | 0.000 | -0.163 | -0.132 |
| np.sin(2 * np.pi * time) | 0.0282 | 0.008 | 3.511 | 0.001 | 0.012 | 0.044 |
| np.cos(2 * np.pi * 2 * time) | 0.0567 | 0.008 | 7.077 | 0.000 | 0.041 | 0.073 |
| np.sin(2 * np.pi * 2 * time) | 0.0591 | 0.008 | 7.371 | 0.000 | 0.043 | 0.075 |
| Omnibus: | 0.996 | Durbin-Watson: | 1.099 |
|---|---|---|---|
| Prob(Omnibus): | 0.608 | Jarque-Bera (JB): | 0.908 |
| Skew: | -0.193 | Prob(JB): | 0.635 |
| Kurtosis: | 2.959 | Cond. No. | 1.11e+06 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.11e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
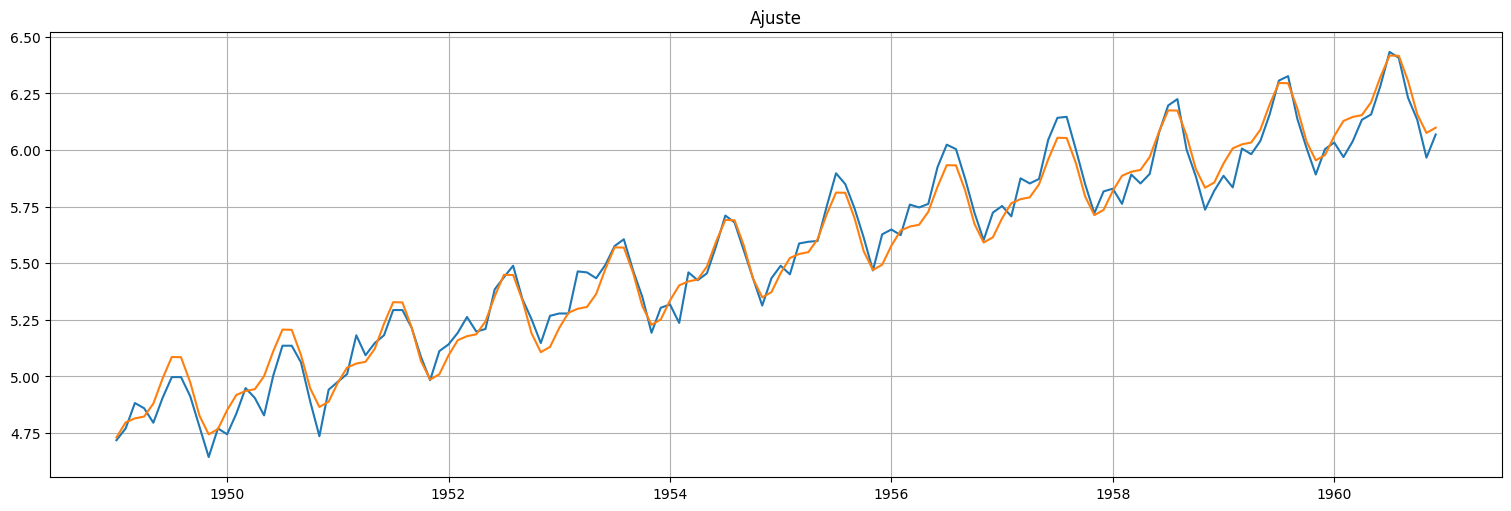
logair.plot()
fit.fittedvalues.plot()
plt.title("Ajuste");
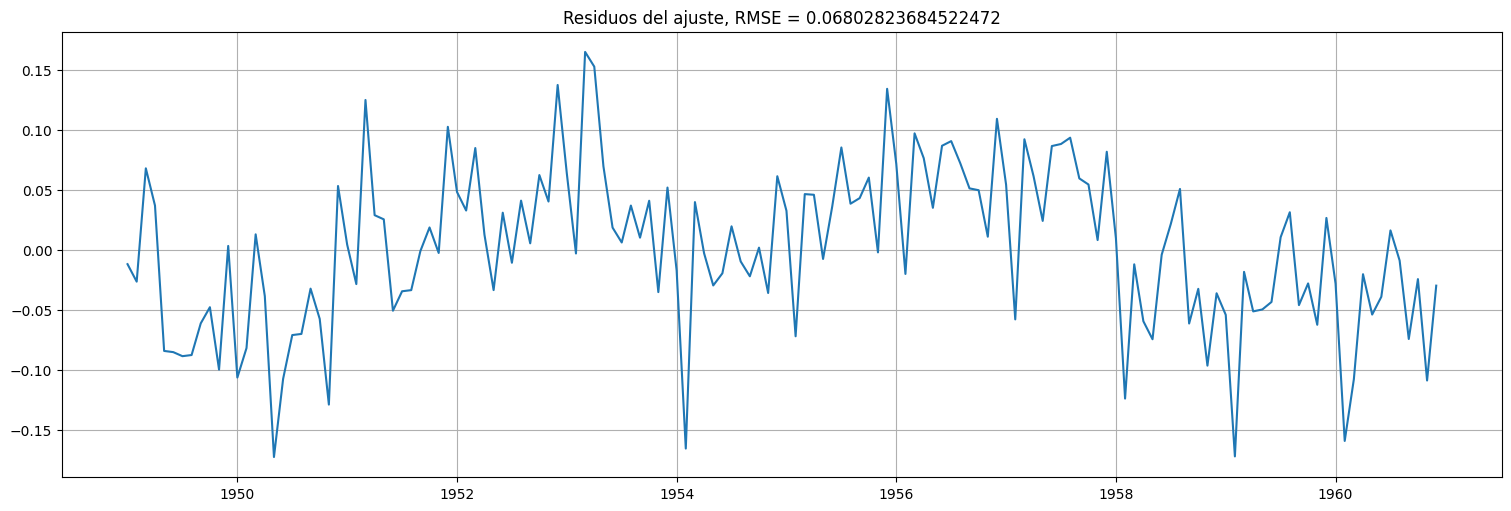
fit.resid.plot()
plt.title(f"Residuos del ajuste, RMSE = {np.sqrt(fit.mse_resid)}");
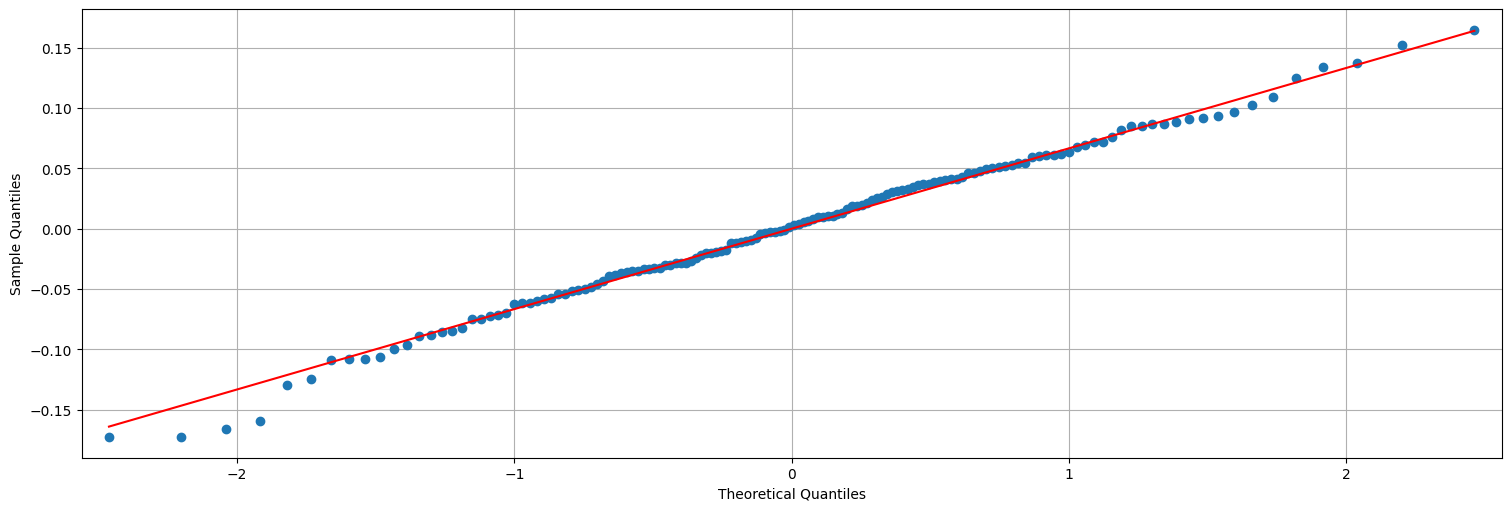
## QQ-plot es una verificación de gaussianidad.
sm.qqplot(fit.resid, line="s");
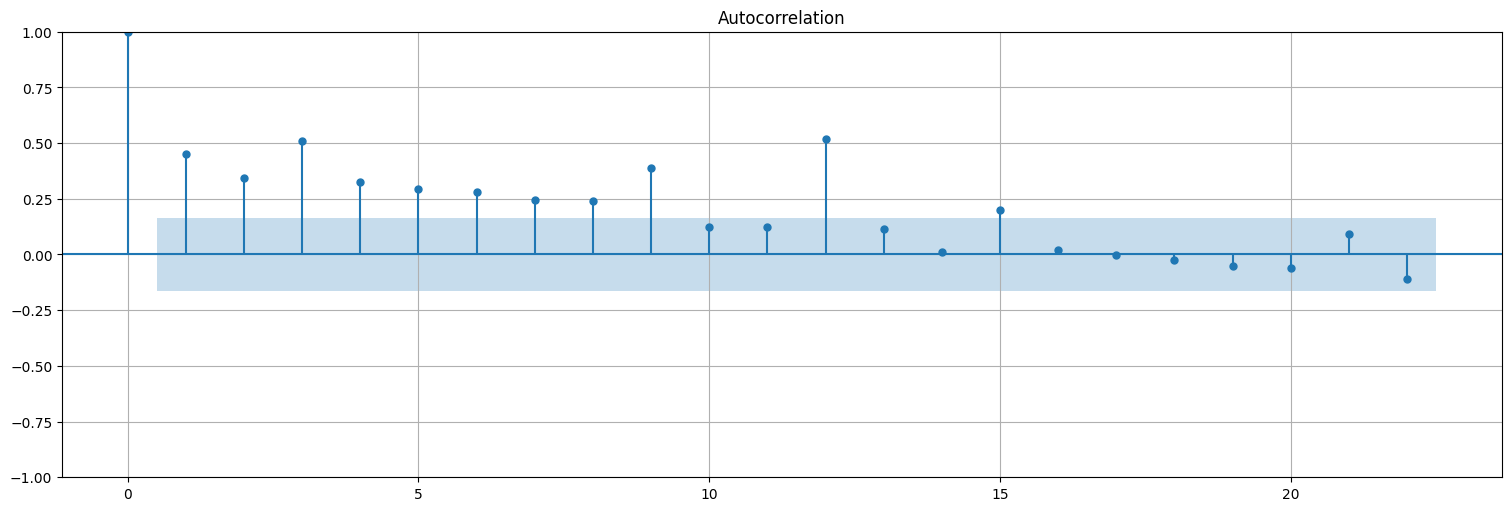
plot_acf(fit.resid.values, bartlett_confint=False);
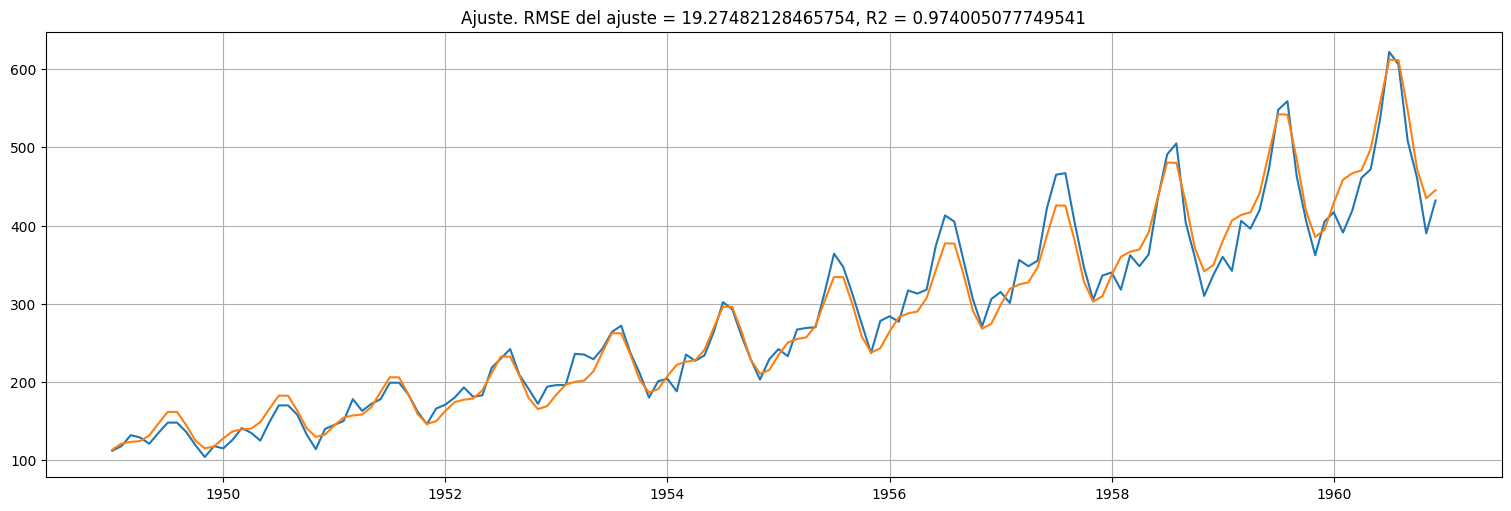
Volvemos ahora a la escala original¶
fitted_values = np.exp(fit.fittedvalues)
air.plot()
fitted_values.plot()
rmse = np.std(air-fitted_values)
R2 = (np.var(air)-np.var(air-fitted_values))/np.var(air)
plt.title(f"Ajuste. RMSE del ajuste = {rmse}, R2 = {R2}");
Ejercicio¶
Análisis frecuencial del fenómeno del niño (serie \(soi\)).¶
En este ejercicio, se busca explorar la naturaleza periódica de \(S_t\), la serie SOI ya analizada.
Quitar la tendencia a las serie mediante una regresión lineal en la componente tiempo. ¿Hay una tendencia significativa en la temperatura de superficie?
Calcular el periodograma para la serie sin tendencia (residuos) de la parte anterior. Identificar las frecuencias principales (una obvia es la anual). ¿Cuál es el ciclo probable del fenómeno del Niño que refleja el pico más pequeño?